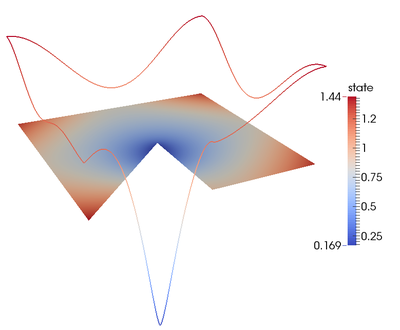
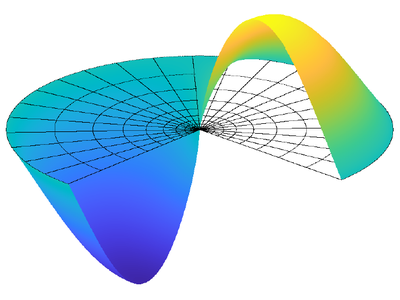
Im Bereich der numerischen Analysis wird zu anisotropen finiten Elementen, zur Diskretisierung von Optimalsteuerproblemen und zu Eigenwerten von Differentialoperatoren geforscht.

 

Anisotrope finite Elemente

fichera.png

Die Verwendung anisotroper finiter Elemente ist besonders effizient wenn die gesuchte Lösung anisotrope Besonderheiten aufweist wie Kantensingularitäten oder Randschichten. In diesem Forschungsfeld werden am IMCS vor allem die Diskretisierungsfehler untersucht und sowohl a priori als auch a posteriori Fehlerabschätzungen hergeleitet.

Ansprechpartner am IMCS
Schüsselpublikationen
  • Apel, T. (1999): Anisotropic finite elements: Local estimates and applications. Teubner, Stuttgart.
  • Apel, T., Lombardi, A. L., Winkler, M. (2014): Anisotropic mesh refinement in polyhedral domains: error estimates with data in L2(Omega). ESAIM: Math. Model. Numer. Anal. 48(4): 1117-1145.
  • Apel, T.; Kempf, V. (2020): Brezzi-Douglas-Marini interpolation of any order on anisotropic triangles and tetrahedra, SIAM J. Numer. Anal., 58(3): 1696-1718.
Aktuelle Projekte
  • Anisotrope Diskretisierung mit isogeometrischer Analysis (IGA)
Abgeschlossene Projekte

 

Diskretisierung von Optimalsteuerproblemen

solution_l2.png

Bei der Optimalsteuerung mit partiellen Differentialgleichungen werden die Daten so bestimmt, dass die Lösung gewünschte Eigenschaften hat. Am IMCS beschäftigen wir uns mit der Diskretisierung solcher Aufgaben, passen vor allem die Diskretisierung an die Problemstellung an und schätzen den Diskretisierungsfehler ab.

Ansprechpartner am IMCS
Schüsselpublikationen
  • Apel, T., Pfefferer, J., Rösch, A. (2014): Locally refined meshes in optimal control for elliptic partial differential equations - an overview. In: G. Leugering, P. Benner, S. Engell, A. Griewank, H. Harbrecht, M. Hinze, R. Rannacher, and S. Ulbrich (eds.): Trends in PDE Constrained Optimization. International Series of Numerical Mathematics 165. Birkhäuser, Basel, pp. 285-302.
  • Apel, T., Mateos, M., Pfefferer, J., Rösch, A. (2015): On the regularity of the solutions of Dirichlet optimal control problems in polygonal domains, SIAM J. Control Optim. 53, 3620–3641.
  • Apel, T., Pfefferer, J., Rogovs, S., Winkler, M. (2018): L∞-error estimates for Neumann boundary value problems on graded meshes. IMA J. Numer. Anal. 40, 474–497.
Aktuelle Projekte
Abgeschlossene Projekte

 

Eigenwerte von Differentialoperatoren

Eigenmode_circularsector_gradedmesh.png

Die Lösung von Differentialgleichungen kann oft durch eine Reihe dargestellt werden, wobei ein Faktor der Reihenglieder durch Eigenfunktionen von Differentialoperatoren dargestellt wird. Man denke zum Beispiel bei Schwingungsproblemen an die Eigenschwingformen. Am IMCS entwickeln wir angepasste Diskretisierungen für solche Probleme und beweisen deren Effizienz.

Ansprechpartner am IMCS
Schüsselpublikationen
  • Apel, T., Sändig, A.-M., Solov'ev, S.I. (2002): Computation of 3D vertex singularities for linear elasticity: Error estimates for a finite element method on graded meshes. Math. Model. Numer. Anal., 36:1043-1070.
  • Apel, T., Mehrmann, V., Watkins, D. (2002): Numerical solution of large scale structured polynomial or rational eigenvalue problems. In: F. Cucker, R. DeVore, P. Olver, and E. Süli, editors, Foundations of Computational Mathematics, Minneapolis 2002, volume 312 of Lecture Note Series, Cambridge, 2004. London Mathematical Society, Cambridge University Press.
  • Apel,T., Pester, C. (2005): Clement-type interpolation on spherical domains - interpolation error estimates and application to a posteriori error estimation. IMA J. Numer. Anal., 25, No.2, 310-336.
Aktuelle Projekte
Abgeschlossene Projekte