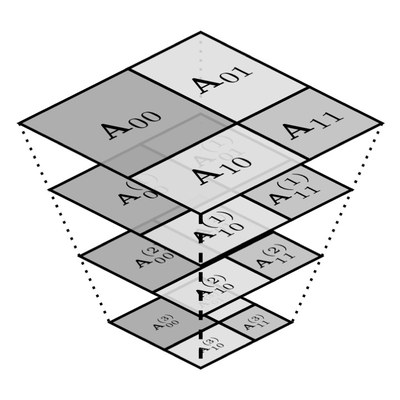
Unsere Forschung auf dem Gebiet des Hochleistungsrechnens konzentriert sich auf Fragen der Vorkonditionierung mittels Mehrgitterverfahren, der Entwicklung von Gebietszerlegungsmethoden und des parallelen Rechnens.
Ansprechpartner am IMCS
Vorkonditionierung und Mehrgitterverfahren
Bei der Lösung großer FEM-Modelle komplexer Probleme sind robuste und problemspezifische iterative Methoden und Vorkonditionierer der Schlüssel für die effiziente Lösung der entstehenden linearen Gleichungssysteme. Da "out-of-the-box" Vorkonditionierungstechniken keine optimale Leistung für komplexe Systeme liefern, entwickelt das IMCS problemspezifische Vorkonditionierungstechniken, indem es die zugrunde liegende Physik in den Entwurf der Vorkonditionierung einbezieht.
Um skalierbare Algorithmen auch für große parallele Simulationen zu erhalten, verwenden und entwickeln die Forschungscodes am IMCS algebraische Mehrgitterverfahren (AMG) im Rahmen von Trilinos/MueLu. Insbesondere entwerfen wir Transfer-Operatoren und Glätter, die auf die Besonderheiten des zugrunde liegenden physikalischen Problems zugeschnitten sind, und stellen Open-Source-Implementierungen unserer Algorithmen über Trilinos/MueLu zur Verfügung.
Das Data Science & Computing Lab betreibt einen HPC-Cluster zur Erprobung der entwickelten Algorithmen.
Schüsselpublikationen
- Firmbach, M., Steinbrecher, I., Popp, A., Mayr, M. (2024): An approximate block factorization preconditioner for mixed-dimensional beam-solid interaction, Computer Methods in Applied Mechanics and Engineering, 431:117256, DOI (Open Access)

- Mayr, M., Berger-Vergiat, L., Ohm, P., Tuminaro, R. S. (2022): Non-invasive multigrid for semi-structured grids, SIAM Journal on Scientific Computing, 44(4): A2734-A2764, DOI

- Wiesner, T.A., Mayr, M., Popp, A., Gee, M.W., Wall, W.A. (2021): Algebraic multigrid methods for saddle point systems arising from mortar contact formulations, International Journal for Numerical Methods in Engineering, 122:3749-3779, DOI (Open Access)
 , arXiv
, arXiv 
Aktuelle Projekte
Gebietszerlegungsmethoden
Methoden der Gebietszerlegung (Domain Decomposition - DD) sind ein wesentlicher Baustein für effizientes paralleles Rechnen und hochleistungsfähige numerische Simulation in der ingenieur-technischen Lösung von partiellen Differentialgleichungen. Am IMCS verwenden wir nicht nur modernste DD-Ansätze zur parallelen Partitionierung und zur Vorkonditionierung iterativer Löser, sondern betreiben auch Spitzenforschung zu Mortar-Methoden für nicht-überlappende Netz- und Feldkopplung. Im Rahmen des parallelen Forschungscodes 4C hat unsere Gruppe eines der weltweit führenden Software-Frameworks für Mortar-Methoden etabliert, dessen Funktionen von der klassischen FEM-Netzkopplung oder der IGA-Patch-Kopplung über duale Lagrange-Multiplikatorräume und dynamische Load Balancing-Verfahren bis hin zur Lösung zahlreicher Ein- und Mehrfeldprobleme reichen, darunter Kontaktmechanik, Thermomechanik und Fluid-Struktur-Interaktion. Unsere Expertise zu Mortar-Methoden hat nicht nur zu neuen wissenschaftlichen Erkenntnissen in Anwendungen wie der Batteriemodellierung oder der Simulation von Schaufel-Scheibe-Verbindung in Flugzeugturbinen beigetragen, sondern fließt im Rahmen einer langjährigen Partnerschaft auch in die Weiterentwicklung kommerzieller FEM-Codes bei ANSYS, Inc. ein.
Schüsselpublikationen
- Mayr, M., Popp, A. (2023): Scalable computational kernels for mortar finite element methods, Engineering with Computers, 39(5):3691-3720, DOI (Open Access)

- Hesch, C., Khristenko, U., Krause, R., Popp, A., Seitz, A., Wall, W.A., Wohlmuth, B.: Frontiers in mortar methods for isogeometric analysis, Preprint, submitted for publication, arXiv

- Wunderlich, L., Seitz, A., Alaydin, M.D., Wohlmuth, B., Popp, A. (2019): Biorthogonal splines for optimal weak patch-coupling in isogeometric analysis with applications to finite deformation elasticity, Computer Methods in Applied Mechanics and Engineering, 346:197-215, DOI

Aktuelle Projekte
- Effiziente numerische Algorithmen für die Lösung von linearen Gleichungssystemen
- Hoch effiziente und parallel skalierbare Mortar-Methoden für Kontakt- und Mehrfeldprobleme
Paralleles Rechnen
 Die heutige Nachfrage nach Simulationsmodellen mit hoher Genauigkeit und Wiedergabetreue bringt in der Regel die Notwendigkeit mit sich, sehr große Berechnungsmodelle auszuführen. Um solche Modelle mit den verfügbaren Hardware-Ressourcen zu kombinieren, befasst sich das IMCS mit speziellen Themen des parallelen Rechnens, um solche Berechnungen auf den heutigen Supercomputern durchzuführen und deren Hardware-Ressourcen effizient zu nutzen. Besondere Forschungsfragen stellen sich bei gemischt-dimensionalen und/oder multiphysikalischen Systemen, bei denen die Arbeitslast der einzelnen Berechnungsdomänen sehr unterschiedlich sein kann und daher maßgeschneiderte Techniken für die Verteilung der Rechenaufgaben und den Lastausgleich erforderlich sind, um alle verfügbaren Rechenkerne im gleichen Maße zu nutzen. Während traditionell verteilte Speicherarchitekturen und die Message-Passing-Schnittstelle (MPI) für die Kommunikation zwischen den Knoten im Mittelpunkt stehen, spielen die Parallelisierung auf den Knoten und Beschleuniger wie grafische Verarbeitungseinheiten (GPUs) eine zunehmende Rolle in Forschung und Anwendungen.
Die heutige Nachfrage nach Simulationsmodellen mit hoher Genauigkeit und Wiedergabetreue bringt in der Regel die Notwendigkeit mit sich, sehr große Berechnungsmodelle auszuführen. Um solche Modelle mit den verfügbaren Hardware-Ressourcen zu kombinieren, befasst sich das IMCS mit speziellen Themen des parallelen Rechnens, um solche Berechnungen auf den heutigen Supercomputern durchzuführen und deren Hardware-Ressourcen effizient zu nutzen. Besondere Forschungsfragen stellen sich bei gemischt-dimensionalen und/oder multiphysikalischen Systemen, bei denen die Arbeitslast der einzelnen Berechnungsdomänen sehr unterschiedlich sein kann und daher maßgeschneiderte Techniken für die Verteilung der Rechenaufgaben und den Lastausgleich erforderlich sind, um alle verfügbaren Rechenkerne im gleichen Maße zu nutzen. Während traditionell verteilte Speicherarchitekturen und die Message-Passing-Schnittstelle (MPI) für die Kommunikation zwischen den Knoten im Mittelpunkt stehen, spielen die Parallelisierung auf den Knoten und Beschleuniger wie grafische Verarbeitungseinheiten (GPUs) eine zunehmende Rolle in Forschung und Anwendungen.
Schlüsselpublikationen
- Firmbach, M., Steinbrecher, I., Popp, A., Mayr, M. (2024): An approximate block factorization preconditioner for mixed-dimensional beam-solid interaction, Computer Methods in Applied Mechanics and Engineering, 431:117256, DOI (Open Access)

- Mayr, M., Popp, A. (2023): Scalable computational kernels for mortar finite element methods, Engineering with Computers, 39(5):3691-3720, DOI (Open Access)