| Project name | Funding Period |
|---|---|
| 2024 - 2027 | |
| 2023 - 2025 | |
| 2022 - 2026 | |
| Multi-scale algorithms and simulation for the patient-specific optimization of endovascular interventions in cerebral aneurysms | 2021 - 2027 |
| Multi-scale modelling of thermomechanical frictional contact for complex problems in engineering | 2021 - 2025 |
| Efficient numerical algorithms for solving systems of linear equations | 2021 - 2026 |
| 2021 - 2024 | |
| Use of eigenfrequencies for the identification of cracks | 2021 - now |
| Combination of Isogeometric Analysis, Finite Element Methods, and Embedded Mesh Coupling Methods for contact problems | 2021 - 2025 |
| Combination of data- and physics-based methods for hybrid digital twins | 2021 - 2026 |
Stable discretization methods and scalable solvers for embedded
fiber/solid coupling

| Funding Agency | Deutsche Forschungsgemeinschaft (DFG) |
| Funding Period | 2024 - 2027 |
| Project Abstract |
This project targets the development of robust and stable discretization techniques and efficient iterative solvers for mixed-dimensional finite element models of fiber-enhanced continua. Mixed-dimensional finite element models of fiber/solid systems will resolve one-dimensional (1D) fibers with beam models embedded into a three-dimensional (3D) homogeneous solid to deliver a high modeling accuracy and will be innovated by enforcing the coupling constraints via a Lagrange multiplier field to overcome the ill-conditioning of previously used penalty methods. A deep understanding of the interplay between solution algorithms and numerical models will deliver fast and efficient solvers ready for next-generation computing architectures. For the first time, this will employ inf-sup stable Lagrange multiplier spaces in mixed-dimensional fiber/solid models and enable the computational analysis of entire fiber-enhanced components and large systems on supercomputers without suffering from ill-conditioning and the lack of diagonal dominance due to penalty methods. |
| Contact at IMCS |
Dr.-Ing. Matthias Mayr, Dr.-Ing. Ivo Steinbrecher, Dharini Balachandran M.Sc. |
Individual production for precast concrete parts

| Funding Agency |
Bayerisches Verbundforschungsprogramm (BayVFP) |
| Funding Period | 2023 - 2025 |
| Partner |
Institut und Labor für Konstruktiven Ingenieurbau, UniBw München |
| Project Abstract |
Within the scope of the joint project "Individuelle Fließfertigung für Betonfertigteile" (IFB), a continuous digital process chain between planning and manufacturing of reinforced concrete components is being created. At the same time, modular manufacturing solutions are being developed using robotics and 3D printing. The main contribution of IMCS is the optimization of steel-reinforcements in non-standard reinforced concrete components. Conventional calculation methods result in a conservative dimensioning of such components and thus in a non-optimal use of resources. The approach developed at IMCS is based on state-of-the-art mixed-dimensional interaction methods to simulate the composite reinforced concrete as detailed and efficient as possible. This allows the application of shape optimization algorithms for the steel-reinforcements. The research and development work is carried out in close cooperation with strong partners from the Bavarian construction industry (Max Bögl), additive manufacturing (FIT AG) and research (Institut und Labor für Konstruktiven Ingenieurbau, UniBw München). |
| Contact at IMCS |
Controllable metamaterials and smart structures (COMET)

| Funding Agency | Deutsche Forschungsgemeinschaft (DFG) |
| Funding Period | 2022 - 2026 |
| Partners | |
| Project Abstract |
This project investigates metamaterial properties of locally periodic structures constituted by conventional and smart materials. Smart materials distinguish themselves from standard passive metamaterials by controllability through electroactive components and time-space alternating geometrical layouts. Controllable and adaptive structures equipped with embedded actuators and sensors connected to electric circuits provide a higher level of multi-functionality such as the capability of vibration and wave propagation control, shape morphing, or modifying stiffness in space and time. The research work is embedded into an international consortium and will be conducted in close collaboration with scientific partners at the Czech Academy of Sciences in Prague (Czech Republic) and at the University of West Bohemia in Pilsen (Czech Republic). |
| Contact at IMCS |
Multi-scale algorithms and simulation for the patient-specific optimization of endovascular interventions in cerebral aneurysms

| Funding Agency | DFG Priority Program 2311 |
| Funding Period | 2021 - 2024 |
| Partner | Chair for Numerical Mathematics, TU Munich Department of Neuroradiology, University Hospital rechts der Isar, TU Munich |
| Project Abstract |
Within this project embedded into the DFG Priority Program 2311, a continuum mechanics approach is being developed for the simulation of the endovascular intervention in cerebral aneurysms with devices such as coils, Woven EndoBridges (Web) or flow diverters. It targets the patient-specific improvement of cerebral aneurysm treatment through predictive simulation and optimization.
IMCS is actively involved in the numerical modeling of the different devices and the involved biochemical processes of blood coagulation in the aneurysm cavity. In collaboration with the project partners, the device and coagulation models will be coupled to a Lattice-Boltzman-based arterial model of the blood flow to predict the long-term treatment outcome and quantify treatment success.
|
| Contact at IMCS |
Multi-scale modelling of thermomechanical frictional contact for complex problems in engineering

| Funding Agency | Deutscher Akademischer Austauschdienst (DAAD) Ministero dell'Istruzione dell'Università e della Ricera (MIUR) |
| Funding Period | 2018 - 2020, 2021 - 2025 |
| Partners | MUSAM Lab, IMT School for Advanced Studies Lucca, Italy (Prof. Paggi) |
| Project Abstract |
This project aims to develop an efficient two-scale numerical scheme integrating implicit finite element (FEM) computations at the macro-scale and the boundary element method (BEM) at the micro-scale for the accurate solution of frictional and thermomechanical contact problems with microscopic interface roughness. The whole range of frictional regimes, from full stick over stick-slip transitions to full sliding, will be handled as well as any complex loading path. The two-scale model will be compared with a fully resolved 3D FEM model using high-performance computing (HPC) techniques. Frictional contact problems are relevant in many engineering and physics research areas. In mechanical engineering, they arise in configurations such as wheel-rail contact, bearings, brakes or wheel-asphalt contact. Friction is also of interest for the interaction between soil and pile foundations in civil and geotechnical engineering applications, and in biomechanics the relative motion in hip-joint prostheses leads to abrasive wear. In all these scenarios, the interface between bodies in contact is not microscopically flat, but its roughness presents multi-scale features that influence the deformation and the stress states in the material. The project includes the development of a micro-scale BEM software named MIRCO (hosted on GitHub), which is an acronym for MUSAM-IMCS Rough Contact cOde. MIRCO is being actively developed and is open-source. It can be utilized as an independent rough surface contact solver or as a a library in other FEM software packages. |
| Contact at IMCS | Dr.-Ing. Ivo Steinbrecher, Rishav Shaw M.Sc. |
Efficient numerical algorithms for solving systems of linear equations
| Funding Agency | Zentrum für Digitalisierungs- und Technologieforschung der Bundeswehr (dtec.bw) |
| Funding Period | 2021 - 2026 |
| Partners | Institutes of dtec.bw project HPC.bw |
| Project Abstract | Efficient numerical algorithms play a crucial role in modern simulation software when solving problems in biomechanics, mechanical and civil engineering. In particular, the solution of systems of linear equation in the context of multiphysics problems represents a challenge in which scalable preconditioners play a critical part. Within the research project, approaches for handling the problem-specific block structure of the underlying matrix as well as novel algebraic multigrid approaches are developed. This includes the development of block and single field smoothers, as well as new methods for coarse grid correction. The multigrid framework MueLu and the block preconditioners based on Teko serve as the software environment. Both software packages are embedded in the open source library Trilinos in order to realize distributed parallel computations on state-of-the-art hardware. On the one hand, the developed methods are used in the parallel simulation of beam-solid problems and heterogeneous materials, as occurring in the interaction of concrete and reinforcing steel. On the other hand, the new methods are utilized for the calculation of fluid-solid interactions from biomechanics. |
| Contact at IMCS |
Highly efficient and parallel scalable mortar methods for contact and multi-field problems
| Funding Period | 2021 - now |
| Partners | 4C-project partners at TU Munich and Helmholtz center Hereon |
| Project Abstract |
In this PhD project, we will advance the coupling of multi-physics problems using mortar finite element methods with a particular focus on the application in nonlinear contact mechanics. Due to the intrinsically nonlinear nature of the introduced constraints at the contact boundary, significantly increased requirements arise for, among other things, contact search algorithms, nonlinear solvers, optimal preconditioning of linear systems of equations, a fully consistent linearization of the problem for implicit time integration, and Mortar-specific operations such as the computation of the mesh intersection at the contact surface within each Newton iteration. |
| Contact at IMCS | Dr.-Ing. Matthias Mayr, Christopher Steimer M.Sc. |
Use of eigenfrequencies for the identification of cracks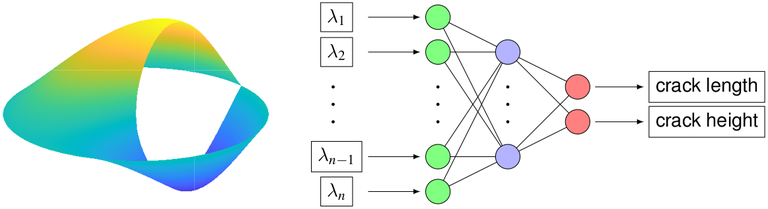
| Funding Period | 2021 - now |
| Project Abstract |
The project focuses on the approximate calculation of eigenvalues of various differential operators on areas with cracks using isogeometric analysis. Methods are to be developed that allow the simulated eigenvalues to represent as accurately as possible the eigenfrequencies of test objects with cracks that can be measured in practice, and also to show corresponding convergence results. Subsequently, these natural frequencies shall be used to identify the crack, i.e., to determine the shape of the crack. This inverse problem is to be solved with a neural network, for the training of which we need simulation data of as high quality as possible in order to be able to guarantee a meaningful application in practice. |
| Contact at IMCS |
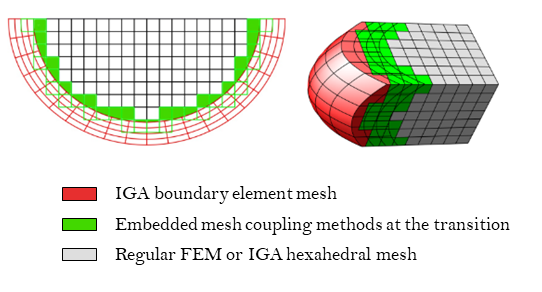
Combination of Isogeometric Analysis, Finite Element Methods, and Embedded Mesh Coupling Methods for contact problems
| Funding Agency | Deutsche Forschungsgemeinschaft (DFG), Internal funds |
| Funding Period | 2021 - now |
| Project Abstract |
In the last years, contact formulations have mostly been developed using the classical Finite Element Method (FEM). However, a typical finite element mesh cannot provide a continuous normal vector field due to the C0 continuity at element intersections. A common solution is to refine the mesh at the contact boundary, which leads to an unnecessary extension of the refined elements into the domain volume. To achieve a higher-order continuity on the contact boundary, contract formulations using Isogeometric Analysis (IGA) have been proposed more recently. These typically use NURBS shape functions for the geometry description as well as the approximation of the solution field. However, the NURBS elements again reach into the domain volume, where their higher-order continuity do not necessarily offer more advantages (due to the reduced regularity of contact problems) but rather cause additional computational costs.
|
| Contact at IMCS | Dr.-Ing. Ivo Steinbrecher, Eugenia Gabriela Loera Villeda M.Sc. |
Combination of data- and physics-based methods for hybrid digital twins
| Funding Agency | Zentrum für Digitalisierungs- und Technologieforschung der Bundeswehr (dtec.bw) |
| Funding Period | 2021 - 2026 |
| Partners | Institutes of dtec.bw project RISK.twin within research center RISK |
| Project Abstract |
In this project, methods for hybrid digital twins of critical infrastructure are investigated and developed. The main focus is the combination of physics-based modeling using Finite Element Methods (FEM) and data-based modeling with machine learning techniques. The first application case are steel-reinforced concrete bridges. On the physics-based modeling side, a mixed-dimensional FEM model for steel-reinforced concrete components is developed. Complementary, variants of neural networks are investigated. Both are combined to improve the material model with measurement data and obtain a reduced order model of the physical system. Still, attention is paid to generality and application independence of the methods, so that the developed techniques can also be used by the project partners. New algorithms are implemented in the form of an in-house software solution. An associated hardware platform for high performance computing is provided at the Data Science & Computing Lab. |
| Contact at IMCS | Dr.-Ing. Daniel Wolff, Bishr Maradni M.Sc., Tarik Sahin M.Sc. |