Our research on computational mechanics focuses on issues of contact and interface mechanics, mixed-dimensional modeling, and coupled multi-physics.

 

Contact and Interface Mechanics

IMCS is internationally acknowledged for innovative research in the field of computational contact interface mechanics.  Our efforts encompass the entire spectrum from micromechanical modeling (e.g. rough surfaces) and tribology (e.g. lubrication) to robust discretization schemes for large deformations (e.g. FEM, IGA) and efficient solution algorithms (e.g. semi-smooth Newton). One particular focus are mortar finite element methods, where contributions range from the mathematical foundations of contact formulations (e.g. stable Lagrange multiplier spaces) to engineering practice and high-performance computing (e.g. algebraic multigrid). Nonlinear beam-to-beam and beam-to-solid contact formulations for the efficient modeling of fiber-based systems round off our unique competence profile. The group carries out both fundamental research (e.g. DFG funding) and application-driven projects including successful industry collaborations.

Contacts at IMCS

• Prof. Dr.-Ing. Alexander Popp
• Dr.-Ing. Matthias Mayr
• Dr.-Ing. Ivo Steinbrecher

Key Publications

• Bonari, J., Marulli, M.R., Hagmeyer, N., Mayr, M., Popp, A., Paggi, M. (2020): A multi-scale FEM-BEM formulation for contact mechanics between rough surfaces, Computational Mechanics, 65(3):731-749, DOI , arXiv 
• Seitz, A., Wall, W.A., Popp, A. (2019): Nitsche's method for finite deformation thermomechanical contact problems, Computational Mechanics, 63:1091-1110, DOI 
• Popp, A., Wriggers, P. (Eds.) (2018): Contact Modeling for Solids and Particles, CISM International Centre for Mechanical Sciences 585, Springer International Publishing, Link 
• Meier, C., Wall, W.A., Popp, A. (2017): A unified approach for beam-to-beam contact, Computer Methods in Applied Mechanics and Engineering, 315:972-1010, DOI 
• Popp, A., Wohlmuth, B.I., Gee, M.W., Wall, W.A. (2012): Dual quadratic mortar finite element methods for 3D finite deformation contact, SIAM Journal on Scientific Computing, 34:B421-B446, DOI 

Current Projects

• Multi-scale modelling of thermomechanical frictional contact for complex problems in engineering
• Highly efficient and parallel scalable mortar methods for contact and multi-field problems
• Combination of Isogeometric Analysis, Finite Element Methods, and Embedded Mesh Coupling Methods for contact problems​

Completed Projects

• A Novel Smooth Discretization Approach for Elasto-Plastic Contact of Solid Bodies and Thin-Walled Structures

• Robust Simulation Methods for Contact, Friction, Wear and Fatigue in Blade-to-Disc Joints in Aircraft Engines

 

Mixed-Dimensional Modeling

Mixed-dimensional problems typically arise in continuum mechanics when high aspect ratio features, such as 1D reinforcing fibers or 2D sheets, are embedded into an ambient 3D domain, and when the physical processes on domains of different dimensionality have non-negligible interactions. Truly mixed-dimensional problems (e.g. 1D-3D or 2D-3D) come with a myriad of challenges to both their theoretical formulation as well their computational treatment, yet they are of utmost importance for many modern engineering applications. At IMCS, we develop sophisticated numerical methods and high-fidelity models for a wide range of mixed-dimensional problems, with the current focus being fiber-reinforced materials in solid mechanics as well as fluid-structure interaction of slender structures in biomedical flows. Our group is also at the forefront of current research regarding tailored solvers (e.g. algebraic multigrid) and parallel software development.

Contacts at IMCS

• Prof. Dr.-Ing. Alexander Popp
• Dr.-Ing. Ivo Steinbrecher
• Dr.-Ing. Matthias Mayr

Key Publications

• Hagmeyer, N., Mayr, M., Popp, A. (2024): A fully coupled regularized mortar-type finite element approach for embedding one-dimensional fibers into three-dimensional fluid flow, International Journal for Numerical Methods in Engineering, published online ahead of print, e7435, 2024, DOI (Open Access) , arXiv 
• Hagmeyer, N., Mayr, M., Steinbrecher, I., Popp, A. (2022): One-way coupled fluid-beam interaction: Capturing the effect of embedded slender bodies on global fluid flow and vice versa,  Advanced Modeling and Simulation in Engineering Sciences, 9:9, DOI (Open Access) , arXiv

• Steinbrecher, I., Popp, A., Meier, C. (2021): Consistent coupling of positions and rotations for embedding 1D Cosserat beams into 3D solid volumes. Computational Mechanics, DOI (Open Access) 
• Steinbrecher, I., Mayr, M., Grill, M. J., Kremheller, J., Meier, C., Popp, A. (2020): A mortar-type finite element approach for embedding 1D beams into 3D solid volumes, Computational Mechanics, 66:1377-1398, DOI (Open Access) 
• Meier, C., Popp, A., Wall, W.A. (2019): Geometrically exact finite element formulations for slender beams: Kirchhoff-Love theory vs. Simo-Reissner theory, Archives of Computational Methods in Engineering, 26:163-243, DOI 

Current Projects

• Mixed-dimensional coupling in solid mechanics
• Mixed-dimensional models for fiber/fluid interaction

Completed Projects

• Bottom-Up Modeling of Stents and Stent Grafts for Endovascular Aortic Repair (EVAR) of Abdominal Aortic Aneurysms

 

Coupled Multi-Physics

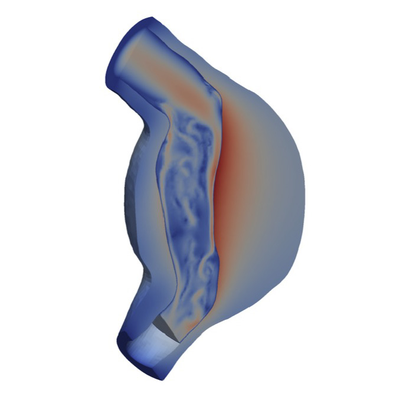
Coupled multi-physics problems are often encountered in science, engineering, or biomedical applications. Their solution requires a profound insight into the interplay of the involved physical mechanisms and numerical methods. Researchers at IMCS address the development of mechanical models, computational methods, and scalable algorithms in the context of coupled multi-physics and interface problems, where exactly this interplay between physics and numerics will facilitate computational robustness and efficiency.

IMCS offers long-standing expertise in discretization techniques for coupling terms as well as the development of efficient and robust solution strategies for coupled problems. Prototype applications are surface-coupled phenomena such as fluid-structure interaction or mixed-dimensional couplings such as fiber/solid or fiber/fluid interaction.

Contacts at IMCS

• Dr.-Ing. Matthias Mayr
• Prof. Dr.-Ing. Alexander Popp

Key Publications

• Hagmeyer, N., Mayr, M., Steinbrecher, I., Popp, A. (2022): One-way coupled fluid-beam interaction: Capturing the effect of embedded slender bodies on global fluid flow and vice versa,  Advanced Modeling and Simulation in Engineering Sciences, 9:9, DOI (Open Access) , arXiv
• Seitz, A., Wall, W.A., Popp, A. (2018): A computational approach for thermo-elasto-plastic frictional contact based on a monolithic formulation employing non-smooth nonlinear complementarity functions, Advanced Modeling and Simulation in Engineering Sciences, 5:5, DOI (Open Access) 
• Mayr, M., Klöppel, T., Wall, W.A., Gee, M.W. (2015): A temporal consistent monolithic approach to fluid-structure interaction enabling single field predictors, SIAM Journal on Scientific Computing, 37(1):B30-B59, DOI , arXiv

Current Projects

• Multi-scale algorithms and simulation for the patient-specific optimization of endovascular interventions in cerebral aneurysms
• Mixed-dimensional models for fiber/fluid interaction

Completed Projects

• Experimental Characterization and Numerical Simulation of the Automated Fiber Placement (AFP) Process for Carbon-Fiber-Reinforced Plastics