Mixed-dimensional models for the interaction between fibers and fluids

| Funding Period | 2018-2023 |
| Project Abstract | This project aims at developing highly efficient mixed-dimensional Mortar finite element methods specifically tailored to model the interaction of very slender rods with the 3-dimensional incompressible Navier-Stokes equations. The interaction of such beam-like structures with fluid flow plays an important role in a broad spectrum of applications varying from biomechanical to industrial processes. Such applications include the interaction of endovascular devices with blood flow and the use of fibrous coverings in flow control for example. At IMCS, we focus on developing specialized 1D-3D coupling approaches that allow for relatively coarse background meshes in order to conserve the benefits — e.g. in terms of the system size, solver time as well as the evaluation of the coupling terms itself — of using a reduced-dimensional structure formulation. Special attention is paid to the application of efficient and scalable parallel algorithms capable of tackling large and complex engineering applications. |
| Contact at IMCS | Dr.-Ing. Matthias Mayr, Nora Hagmeyer M.Sc. |
Mixed-dimensional coupling in solid mechanics
| Period | 2018-2022 |
| Partners | Institute for Computational Mechanics, TU Munich |
| Project Abstract |
In various engineering and biomechanical applications, the integration of slender fibers with three-dimensional bodies significantly enhances the mechanical properties of the overall structure. In this project, novel coupling methods are developed for such problems, where the fibers are explicitly modelled using one-dimensional (1D) beam theories, resulting in a very accurate and efficient numerical formulation. State-of-the-art finite element methods (FEM) are used for the 3D solids. Such approaches are also referred to as mixed-dimensional coupling, as the underlying differential equations are defined on domains with different dimensions. A key advantage of these mixed-dimensional methods is the simplicity of model generation, as the 1D fibers and 3D bodies can be discretized independently of each other. Over the course of this project, coupling methods for embedded fibers in volumes (1D-3D) and fibers connected or in contact with surfaces (1D-2D) based on Mortar/Lagrange multiplier methods have already been successfully developed. |
| Contact at IMCS | Dr.-Ing. Ivo Steinbrecher |
Optimal control problems governed by elliptic variational inequalities
| Funding/Agency | Deutsche Forschungsgemeinschaft (DFG) within the international research training group IGDK 1754 with the title Optimization and Numerical Analysis for Partial Differential Equations with Nonsmooth Structures |
| Funding Period | 2017-2022 |
| Partners | Technische Universität München (Prof. Vexler) Technische Universität Graz (Prof. Steinbach) |
| Project Abstract |
The project deals with optimal control of variational inequalities. A priori error estimates for finite element discretizations of optimal control problems for elliptic variational inequalities and different regularization strategies are considered. Further information can be found here. |
| Contact at IMCS |
Anisotropic pressure-robust discretizations for the Navier-Stokes equations
| Funding Period | 2018-2022 |
| Partners | Weierstrass Institute for Applied Analysis and Stochastics (Priv.-Doz. Dr. Alexander Linke, Dr. Christian Merdon) |
| Project Abstract | The focus of the project is to develop error estimates for discretizations of the Navier-Stokes equations on anisotropically refined meshes, where the velocity error is independent of the pressure approximability. Further information can be found here. |
| Contact at IMCS |
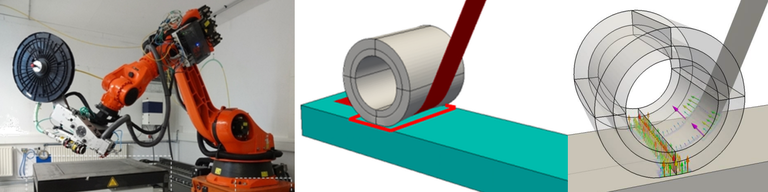
Experimental Characterization and Numerical Simulation of the Automated Fiber Placement (AFP) Process for Carbon-Fiber-Reinforced Plastics
| Funding/Agency | Deutsche Forschungsgemeinschaft (DFG), PO 1883/3-1 |
| Funding Period | 2017-2021 |
|
Partners |
Institute for Carbon Composites, TU Munich (Prof. Drechsler) Institute for Comutational Mechanics, TU Munich (Prof. Wall) |
| Project Abstract | The efficient, high-quality and reproducible production of thermoplastic fiber-reinforced plastic components requires automated manufacturing processes. Due to its load-path oriented deposition of fibers to near-net-shape components, automated fiber placement (AFP) has particularly great potential. With proper temperature control during thermoplastic AFP (TP-AFP) in-situ consolidation is possible, i.e. a consolidation in place of the process without downstream thermosetting. However, the understanding of the process is still far from reaching the level of maturity necessary for a broad industrial application of TP-AFP. For example, it is still difficult today to define suitable process windows for the most important key parameters such as laser power, velocity and compaction pressure so that a consistently high quality of components is assured. In particular, the prediction of residual stresses and distortion is only solved insufficiently and process calibration is often based on a trial-and-error method. The reasons for this discrepancy between low prediction accuracy and high industrial demands can likewise be ascribed to possibilities of experimental characterization and modeling and simulation that are not yet maxed out. Therefore, the aim of this project is to improve process understanding in the area of TP-AFP fundamentally through novel experimental studies and methods of numerical simulation. |
| Contact at IMCS | Prof. Dr.-Ing. Alexander Popp |
Bottom-Up Modeling of Stents and Stent Grafts for Endovascular Aortic Repair (EVAR) of Abdominal Aortic Aneurysms

| Funding/Agency | Daimler and Benz Foundation |
| Funding Period | 2016-2018 |
| Partners | Institute of Industrial Science, The University of Tokyo, Japan (Prof. Oshima) |
| Project Abstract | Arterial stent placement has become a very important and successful intervention in vascular surgery. One of the most common scenarios includes so-called self-expandable stent grafts composed of a special fabric graft and a metal stent mesh. Stent grafts are used in endovascular aortic repair (EVAR) to support weak localized bulges (aneurysms) in an artery being at risk of rupture, most commonly for abdominal aortic aneurysms (AAA). Over the last decade, an enormous thrust of research regarding the computational analysis of biomedical engineering problems in general, and regarding vascular mechanics and AAA in particular has taken place. While significant progress has been made, the computational analysis of AAA stent grafts using finite element methods (FEM) is still not predictive enough to give specific advice to vascular surgeons on how to optimally place the device during EVAR. Possible risks, which are still far from being fully understood, include a movement of stents away from the desired location (migration), leaking of blood around stent grafts (endoleakage) and damage of the arterial wall caused by the stent itself. The main objective of this project is the development, implementation and validation of new innovative FEM simulation tools for AAA stent grafts based on a bottom-up modeling approach. All relevant micro-geometrical and mechanical features of the complex stent graft designs will be included into the new models, thus allowing for a significantly increased accuracy of stent expansion and placement simulations. |
| Contact at IMCS | Prof. Dr.-Ing. Alexander Popp |
A Novel Smooth Discretization Approach for Elasto-Plastic Contact of Solid Bodies and Thin-Walled Structures
| Funding/Agency | Deutsche Forschungsgemeinschaft (DFG), PO 1883/1-1 in the framework of the Priority Programme SPP 1748 |
| Funding Period | 2014-2017 |
| Partners | Institute of Numerical Mathematics, TU Munich (Prof. Wohlmuth) |
| Project Abstract | This project aimed at introducing a new discretization method for contact of bulky and thin-walled structures exhibiting pronounced geometrical and material nonlinearities. The resulting smooth contact approach goes beyond traditional smoothing procedures with regard to a sound mathematical basis, but at the same time retains the simplicity of low-order finite element discretizations in the bulk of the computational domain. Volume and contact surface discretizations are strictly separated, but interconnected via variationally consistent coupling operators based on generic biorthogonal Lagrange multiplier bases. This new approach promises to offer maximal flexibility with regard to a smooth surface discretization (e.g. using higher-order FEM, Hermite interpolation, splines or NURBS) and a completely independent volume discretization (e.g. using low-order non-conforming FEM, EAS or F-Bar techniques). In addition, an integrated treatment of contact and friction as well as finite strain plasticity based on so-called nonlinear complementarity functions and semi-smooth Newton methods has been developed, which offers a superior robustness as compared with traditional radial return mapping schemes. |
| Contact at IMCS | Prof. Dr.-Ing. Alexander Popp |
Robust Simulation Methods for Contact, Friction, Wear and Fatigue in Blade-to-Disc Joints in Aircraft Engines
| Funding/Agency | Rolls-Royce Deutschland Ltd & Co KG in the framework of the German Aviation Research Program (BMWi) |
| Funding Period | 2007-2017 |
| Partners | Rolls-Royce plc (U.K.) |
| Project Abstract | Long-term industry collaboration (over 10 years) with several sub-projects that were concerned with robust discretization schemes and solution algorithms for contact problems in turbine blade-to-disc joints. New computational methods for domain decomposition, frictional contact, fretting wear and fretting fatigue have been developed, validated and integrated into the industrial partner's in-house finite element code. Consulting on high-performance computing (HPC). |
| Contact at IMCS | Prof. Dr.-Ing. Alexander Popp |