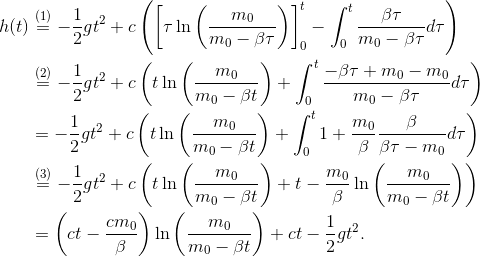Raketenflug

Am Beispiel eines senkrechten Raketenfluges wollen wir ein weiteres Optimierungsproblem lösen.

Problem

Gegeben sei eine Rakete, die senkrecht starten soll. Zum Zeitpunkt 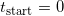befindet sich die Rakete auf dem Boden, hat also die Höhe 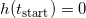. Außerdem befindet sie sich in Ruhe, 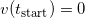, und hat eine Masse .

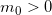Wir wollen den Senkrechtstart vereinfacht mathematisch beschreiben und mithilfe dieses Modells ausrechnen, wie hoch der Treibstoffdurchsatz sein muss, damit die Rakete so hoch wie möglich fliegt.

Dabei muss beachtet werden, dass sich nur Treibstoff mit der Masse 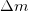in der Rakete befindet.

Modellierung

Als Erstes müssen die Bewegungsgleichungen aufgestellt werden.

Unter einer Bewegungsgleichung versteht man eine mathematische Gleichung oder auch ein Gleichungssystem, die die räumliche und zeitliche Entwicklung eines mechanischen Systems vollständig beschreibt. (Wikipedia)

Uns interessiert vor allem die Höhe der Rakete. Aus dem Physikunterricht wissen wir, dass die Änderung der Höhe bei senkrechtem Flug der Geschwindigkeit entspricht.

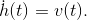
Aber ist dadurch das System schon vollständig beschrieben? Nein, da sich die Geschwindigkeit der Rakete mit der Zeit auch verändert. Dazu nehmen wir an, dass der Schub 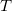vom Treibstoffdurchsatz 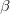abhängt, den wir steuern wollen: 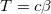. Der Schub ist eine Kraft, und damit ist Schub geteilt durch Raketenmasse eine Beschleunigung und wir können auch die Änderung der Geschwindigkeit angeben

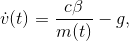
wobei 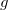die Erdbeschleunigung ist, die der Beschleunigung durch den Schub entgegenwirkt. Unser System ist aber immer noch nicht vollständig beschrieben, da sich die Masse unserer Rakete ändert wenn wir Treibstoff verbrauchen. Hier ist der Zusammenhang allerdings sehr einfach beschrieben durch

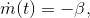
da die Rakete genau um den Treibstoffdurchsatz leichter wird. Dieser ändert sich nicht mit der Zeit, also ist unser System nun vollständig. Wirklich rechnen können wir allerdings mit unseren Bewegungsgleichungen noch nicht. Denn die Ableitungen lassen sich ohne weiteres nicht in die jeweiligen Funktionen einsetzen.

Zuerst bestimmen wir 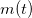durch Integration von 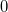bis :

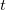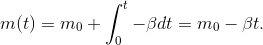
Dieses Ergebnis können wir jetzt in die Gleichung von 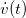einsetzen und auch dort von 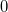bis 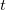integrieren um die Stammfunktion zu finden.

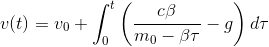
Bei dieser Rechnung müssen wir ein paar Tricks benutzen. Einer davon ist, anstatt 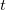innerhalb des Integrals zu benutzen und 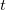als variable obere Grenze zu setzen. Dadurch ist das Ergebnis der Integration genau das 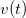was wir suchen. Zuerst trennen wir das Integral auf

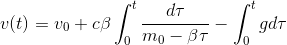
und wir sehen sofort, dass sich das rechte Integral sehr leicht lösen lässt. Das linke Integral kann mithilfe von Substitution (oder einer geeigneten Formelsammlung) gelöst werden, da 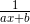ein Standardfall ist. Also erhalten wir im nächsten Schritt

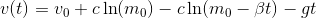
was auch definiert ist, weil wir keine 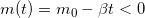zulassen. Eine Rakete wird schließlich auch noch etwas wiegen, sobald der Treibstoff verbraucht ist. Da die Anfangsgeschwindigkeit 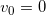ist können wir nun die Rechenregeln für den natürlichen Logarithmus ausnutzen und erhalten schließlich

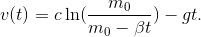
Im letzten Schritt setzen wir unsere Lösung für 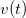in die Differentialgleichung für die Höhe 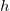ein und integrieren wieder, um die Stammfunktion zu finden:

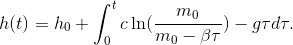
Die Lösung dieses Integrals bedarf einer etwas längeren Rechnung die im Anhang am Ende der Seite ausgeführt wird. Das Ergebnis ist

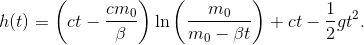
Damit haben wir eine Funktion 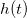die beschreibt, wie sich die Höhe der Rakete verhält, abhängig davon wie wir den Treibstoffdurchsatz  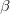wählen.

Lösung

Die Dynamik der Rakete haben wir erfolgreich modelliert. Weiter geht es mit der Lösung des Problems. Wir haben die Gleichung der Höhe in Abhängigkeit von Zeit und gewähltem Treibstoffdurchsatz, aber wir wollen nur den Treibstoffdurchsatz 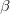wählen. Da wir nur die begrenzte Menge 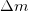an Treibstoff zur Verfügung haben, ist der Zeitpunkt 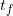, ab dem kein Treibstoff mehr vorhanden ist, festgelegt durch

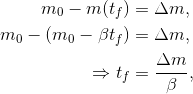
und wir können die Höhe 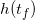zu diesem Zeitpunkt ausrechnen:

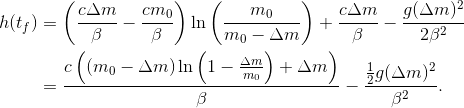
Die Höhe hängt jetzt nur noch vom Treibstoffdurchsatz 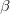ab. Um die Formel lesbarer zu machen schreiben wir

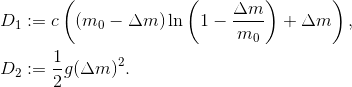
Damit ergibt sich für unsere Zielfunktion

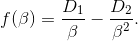
Die Funktion 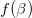beschreibt unsere Höhe in Abhängigkeit von unserem Treibstoffdurchsatz 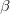. Von dieser Funktion suchen wir das Maximum, dazu bilden wir zuerst die erste Ableitung bezüglich 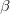und suchen die Nullstellen

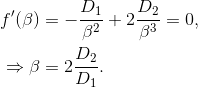
Nun prüfen wir die hinreichende Bedingung für ein Maximum. Dazu bilden wir die zweite Ableitung und setzen die Nullstelle der ersten Ableitung ein

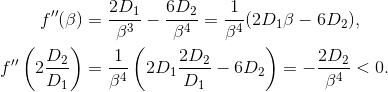
Damit ist gezeigt, dass sich bei 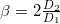 ein lokales Maximum der Funktion 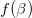befindet. Dieser Wert gibt an, wie hoch der Treibstoffdurchsatz sein muss, damit die Höhe der Rakete in unserem einfachen Modell maximal wird. Der Fall 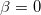, an dem unsere Zielfunktion eine Polstelle aufweist wird ausgeschlossen, da ohne Treibstoffdurchsatz auch der Schub 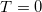ist, und damit kein Flug möglich ist.

Beispiel mit realen Werten

In Bearbeitung

Ungenauigkeiten des Modells

Es ist wichtig darüber nachzudenken, wo unser Modell ungenau ist, damit wir die Ergebnisse richtig interpretieren können.

Einen Fehler machen wir beispielsweise bei der Annahme, dass die Erdbeschleunigung 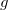konstant ist. Diese Annahme beeinflusst unsere Gleichung 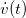. Eigentlich hängt die Erdbeschleunigung aber von der Höhe ab: 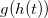. Falls unsere Rakete nicht allzu hoch fliegt, sollte der Fehler allerdings recht klein sein. Würden wir eine nichtkonstante Erdbeschleunigung in unser Modell aufnehmen, wäre es deutlich schwieriger auszurechnen, wie wir die Rakete möglichst hoch fliegen lassen können.

Unser Modell berücksichtigt auch nur einen Treibstofftank, der nicht abgeworfen werden kann. Bei einem Spaceshuttle beispielsweise gibt es einen Außentank und zwei Feststoffbooster (Raketen), die abgeworfen werden, sobald sie nicht mehr benötigt werden, wie man bei diesem YouTube Video zum Space-Shuttle Start sehen kann.

Das verändert natürlich die Masse der Rakete.

Dies waren nur Beispiele für Fehler in unserem Modell. Fallen Ihnen weitere Ungenauigkeiten ein?

Anhang

Berechnung von

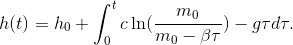
Die Summanden des Integrals werden einzeln berechnet, und wir benutzen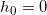

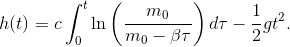
Mit partieller Integration (1), Addition von 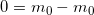(2), der Integrationsregel 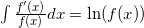(3) und den Rechenregeln des Logarithmus ergibt sich weiter