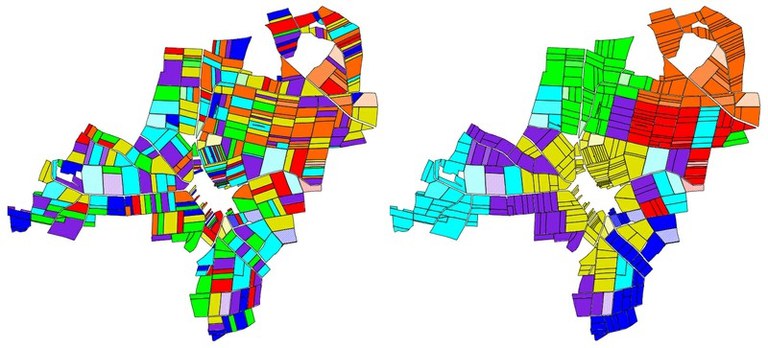
In vielen ländlichen Regionen pflegt eine kleine Zahl von Landwirten eine große Anzahl von kleinen Parzellen, die über eine weite Fläche verstreut liegen. Es resultieren hohe Fahrtkosten und und ein unprofitabler Einsatz der benötigten schweren Maschinen. Abhilfe könnte eine Flurbereinigung schaffen, welche aber häufig unerwünschte Nebenwirkungen mit sich bringt. Wir entwickeln mathematische Modelle und Algorithmen zur Flurbereinigung, welche nicht die Ergebnisse eines klassischen Flurbereinigungs-Prozesses verwenden.

Die zentrale Idee unserer Methoden ist, dass die Struktur der Parzellen in der Region erhalten bleibt. Einige dieser Parzellen werden von den Bauern fixiert und die Übrigen werden, nach speziellen  Zielfunktionen, kombinatorisch neu zugewiesen. Während dieses Prozesses soll jeder Landwirt eine Reihe von Parzellen erhalten, die in etwa der ursprünglichen Gesamtgröße und dem Wert der Parzellen entspricht. Da die Parzellen sich hinsichtlich ihrer Größe und Bonität unterscheiden, erhalten wir ein schwieriges Clustering-Problem unter Nebenbedingungen: Die Entscheidung, ob es eine andere Verteilung der Parzellen gibt, so dass diese Nebenbedingungen erfüllt sind, stellt ein NP-vollständiges Problem dar.

Mit  den Methoden der kombinatorischen Optimierung erhalten wir nachweislich gute und effiziente Approximations-Algorithmen. Im Rahmen dieses Projektes werden zwei Ziele verfolgt: Zum einen die fortlaufende Verbesserung der mathematischen Modelle, die die realen Probleme der Flurbereinigung darstellen, zum anderen die Entwicklung verbesserter Algorithmen für diese Modelle.