Rettungsschwimmerproblem

Das Rettungsschwimmerproblem ist sehr gut geeignet, um die strukturierte Vorgehensweise zur Problemlösung zu zeigen.

Problem

Ein Rettungsschwimmer befindet sich auf einem Strand und sieht einen ertrinkenden Schwimmer. Auf welchem Weg erreicht der Rettungsschwimmer diesen am schnellsten?

Modellierung

Zunächst ist es wichtig, dieses Problem zu modellieren. Wir brauchen also ein Modell bzw. eine formale Beschreibung des Problems. Da wir die kürzeste (minimale) Zeit T in Abhängigkeit des Weges finden wollen, ist das Ziel der Modellierung eine Funktion

T: Weg → Zeit,

von der wir dann das Minimum bestimmen können. Dazu ist es in diesem Fall nützlich, ein Koordinatensystem einzuführen: Der Rettungsschwimmer wird dargestellt durch den Punkt R:(0,5), der Schwimmer durch den Punkt S:(50,-10).

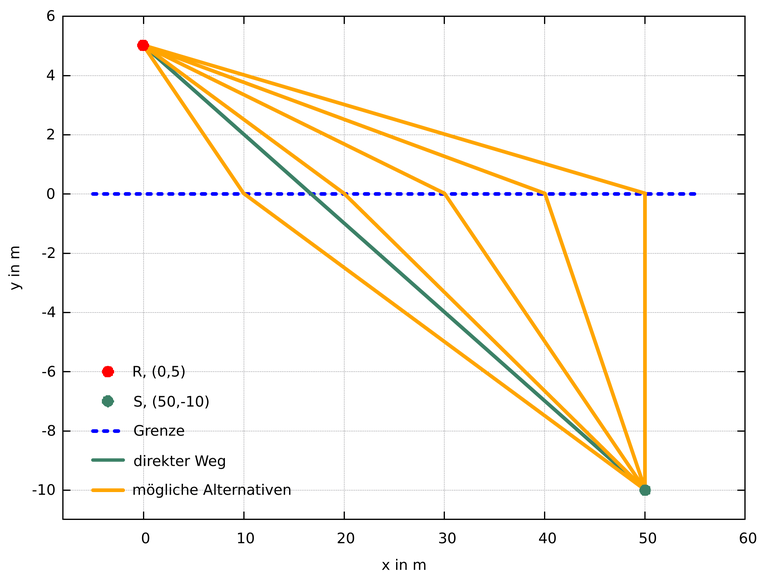
Die x-Achse stellt die Grenze zwischen Strand (oberhalb der x-Achse) und Meer (unterhalb der x-Achse) dar. Auf dem Strand erreicht der Rettungsschwimmer eine Geschwindigkeit von v_s = 16 km/h und im Wasser nur v_w = 4 km/h. Der direkte Weg (grün) ist der kürzeste, aber ist er auch der schnellste? Da in dieser Situation die Geschwindigkeit v_w im Wasser niedriger ist als v_s auf dem Strand, könnte sich ein anderer Weg als schneller erweisen.

Wesentlich unterscheiden sich die unterschiedlichen Wege darin, an welcher Stelle x_in der Rettungsschwimmer in das Wasser geht. Die Zeit, die der Rettungsschwimmer braucht, um zum Punkt S zu gelangen, hängt also von x_in ab und besteht aus zwei Teilen:

T(x_in) = t_Strand(x_in) + t_Meer(x_in)

mit

t_Strand = s_Strand / v_Strand,         t_Meer = s_Meer / v_Meer.

Man kann nun die Strecken s_Strand und s_Meer in Abhängigkeit von x_in ausdrücken. Dabei hilft der Satz des Pythagoras:

s_Strand(x_in) = ( (5 m)² + x_in² )^½,        s_Meer(x_in) = ( (10 m)² + (50 m - x_in)² )^½

Damit kann nun die Gesamtzeit beschrieben werden durch

T(x_in) = ( (5 m)² + x_in² )^½ / v_s + ( (10 m)² + (50 m - x_in)² )^½ / v_w

Lösung

Von dieser Funktion suchen wir jetzt das Minimum. In der grafischen Darstellung von T(x_in) kann man das Minimum ablesen:

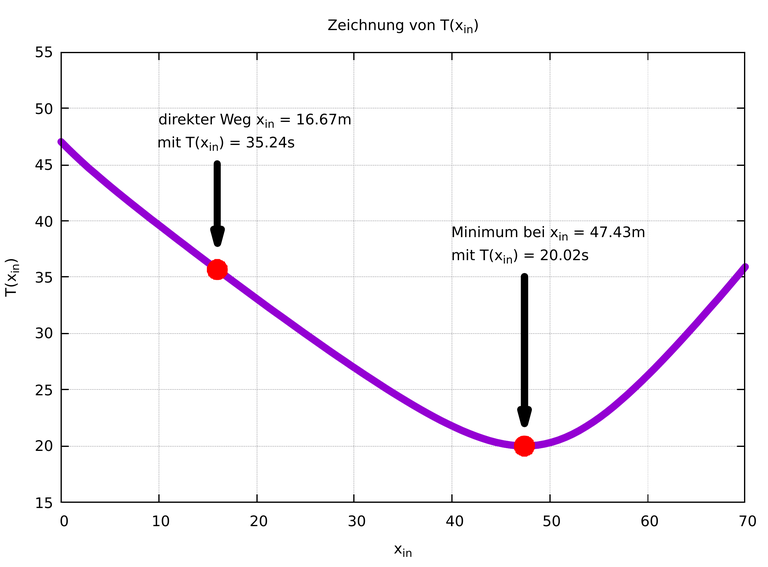
Genauere Lösungen erhält man durch die Suche nach dem Extremwert (hier das Minimum) der Funktion T(x_in). Die Lösung mit x_in = 47,43 m ist hier der zeitlich kürzeste Weg, auch wenn die Gesamtstrecke länger ist. Zum Vergleich: der direkte Weg führt über x_in = 16,67 m in der Zeit T(x_in) = 35,24 s, und wäre damit deutlich langsamer.

Ungenauigkeiten des Modells

Es ist natürlich auch wichtig, sich Gedanken darüber zu machen, wo das Modell Schwächen hat. In unserem Fall wird nicht berücksichtigt, dass der Rettungsschwimmer vermutlich im trockenen Sand langsamer laufen kann als nahe am Wasser, wo der Sand fester ist. Des Weiteren kann der Rettungsschwimmer auch im flachen Meer laufen und muss nicht gleich anfangen zu schwimmen.

Diese Betrachtungen sind immer von Bedeutung, wenn die Ergebnisse einer solchen Berechnung diskutiert werden. Denn aus einem ungenauen Modell gehen auch ungenaue Ergebnisse hervor! Manchmal ist allerdings der Aufwand, ein genaueres Modell zu benutzen und damit auch zu rechnen derart hoch, dass man lieber mit den Ungenauigkeiten lebt.

Beim Rettungsschwimmerproblem wird trotz der Ungenauigkeiten deutlich, dass der direkte Weg im Allgemeinen nicht der schnellste ist und er in diesem Fall einen längeren Weg zugunsten der höheren Geschwindigkeiten wählen sollte.