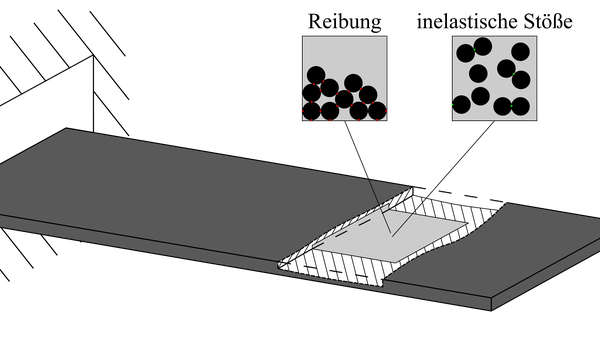
Schematic diagram of an additively manufactured particle damper with the two mechanisms of action of energy dissipation; based on [13] (from [14]).
In recent years, the use of additive manufacturing (AM) in industrial structural applications has gained importance, as AM and in particular the Laser Powder Bed Fusion process (PBF-LB) offers several advantages compared to conventional manufacturing processes [1]. Relevant to the research project presented here are the capabilities for manufacturing integral components on the one hand and lightweight structures on the other. Integral components are designed to consist of as few parts as possible, with each part performing multiple functions [2]. This is advantageous not only from an industrial manufacturing point of view, but also from a component performance point of view, as it increases strength and reduces weight. This is particularly advantageous in the aerospace, automotive, and energy sectors [3]. A high stiffness-to-weight ratio, often desired, can be achieved by topology optimization and its geometrically complex solutions are particularly suitable for fabrication by PBF-LB [4]. Several industrial applications already show that PBF-LB is used to fabricate lightweight, comparatively stiff and integrally designed structural components [5]. But these specific advantages become disadvantages when the components are under vibration, since lightweight structures are more susceptible to vibration [6], rigid structures have lower component damping, and the lack of friction in fasteners reduces the damping properties of integrally designed components [7]. This results in lower component life and higher sound radiation.
One method to counteract these susceptibilities is the use of particle damping. In this passive damping system, the component consists of a fixed (primary) mass and a moving (secondary) particulate mass. This secondary mass can be attached to the primary mass as an outer container or inserted into the primary mass [8]. Under vibration, the secondary mass releases energy through inelastic collisions or friction between the particles or between the particle and the wall, see Fig. 1 [9]. PBF-LB offers the possibility of incorporating particle damping inherently into the design of a component by designing cavities inside the component where unmelted powder remains after fabrication. Following the concept of "complexity for free" [10], Ehlers et al [11] coined the term "damping for free" because this technique does not increase component mass or manufacturing costs compared to a fully molten reference component. However, modeling of conventional and AM particle dampers has not been reliable because the damping characteristics are highly nonlinear and depend on several design parameters such as cavity size, cavity position, excitation amplitude and frequency [12]. To better understand this additive manufacturing application, this subproject fabricated samples with particle damping from the aluminum alloy AlSi10Mg using PBF-LB and tested their damping properties. The exemplary future use case of a turbine blade was considered by choosing a thin and shallow cavity.
Two types of specimens were designed. The two "solid" specimens are completely fused and serve as the basis for the modal parameters. The three "cavity" specimens have the same external geometry as the solid specimens and differ only in having an internal cavity whose position was chosen so that it does not overlap with a nodal point in the first three bending modes. However, a nodal point of the fourth bending mode and the cavity coincide. The dimensions of the specimens and the first four bending modes can be seen in Fig. 2.
The specimens are successively clamped in an electrodynamic shaker to analyze their modal parameters. The system excitation is measured using an accelerometer at the clamp and the system response is measured using scanning laser Doppler vibrometry (SLDV), see Fig. 3. The excitation acceleration is kept constant over all frequencies within a measurement to allow better comparability between modes. After a series of measurements, it is then increased from 100 mm/s2, 200 mm/s2, 400 mm/s2 to 800 mm/s2 per frequency range to determine the nonlinear attenuation properties of particle attenuation mentioned earlier. The distribution of the particles in the cavity before and after the modal analysis is studied by computed tomography (CT).
With this experimental setup, the first four bending modes and the first two torsional modes are excited. The corresponding mode shapes can be seen in Fig. 4. The data of the first bending mode are not considered because large deflections lead to parasitic friction in the restraint, which affects the component damping [13]. The comparison of damping as loss factors of all specimens for all considered bending modes can be seen in Fig. 5. The bending modes show little to no damping effect for the smaller excitation amplitudes. However, for higher excitation amplitudes, the damping effect increases sharply. A positive damping effect can be seen for all bending modes, but most clearly for the third bending mode. The damping of the torsional modes was also analyzed, but no significant damping effect was measured.
The dependence of the damping effect on the mode, the excitation amplitude as well as the specific specimen needs to be further investigated in future studies. Additionally, during the experiments, a settling of the powder in the cavity has been shown to lead to a reduction of the damping over time. This effect, as well as the impact of additive manufacturing on the dispersion of the damping effect, still needs to be investigated in order to create an analytical model to calculate the damping effect.
This research work is funded by dtec.bw – Digitalization and Technology Research Center of the Bundeswehr which we gratefully acknowledge [project FLAB-3Dprint]. dtec.bw is funded by the European Union – NextGenerationEU.
