Publications

Constrained composite optimization and augmented Lagrangian methods

Abstract:

We investigate finite-dimensional constrained structured optimization problems, featuring composite objective functions and set-membership constraints. Offering an expressive yet simple language, this problem class provides a modeling framework for a variety of applications. We study stationarity and regularity concepts, and propose a flexible augmented Lagrangian scheme. We provide a theoretical characterization of the algorithm and its asymptotic properties, deriving convergence results for fully nonconvex problems. It is demonstrated how the inner subproblems can be solved by off-the-shelf proximal methods, notwithstanding the possibility to adopt any solvers, insofar as they return approximate stationary points. Finally, we describe our matrix-free implementation of the proposed algorithm and test it numerically. Illustrative examples show the versatility of constrained composite programs as a modeling tool and expose difficulties arising in this vast problem class.

Reference:

• De Marchi, A., Jia, X., Kanzow, C., and Mehlitz, P.: Constrained composite optimization and augmented Lagrangian methods. Mathematical Programming (2023). DOI 10.1007/s10107-022-01922-4

A Function Approximation Approach for Parametric Optimization

Abstract:

We present a novel approach for approximating the primal and dual parameter-dependent solution functions of parametric optimization problems. We start with an equation reformulation of the first-order necessary optimality conditions. Then, we replace the primal and dual solutions with some approximating functions and find for some test parameters optimal coefficients as solution of a single nonlinear least-squares problem. Under mild assumptions it can be shown that stationary points are global minima and that the function approximations interpolate the solution functions at all test parameters. Further, we have a cheap function evaluation criterion to estimate the approximation error. Finally, we present some preliminary numerical results showing the viability of our approach.

Reference:

• De Marchi, A., Dreves, A., Gerdts, M., Gottschalk, S., Rogovs, S.: A Function Approximation Approach for Parametric Optimization. J Optim Theory Appl 196, 56–77 (2023). DOI 10.1007/s10957-022-02138-4

On a primal-dual Newton proximal method for convex quadratic programs

Abstract:

This paper introduces QPDO, a primal-dual method for convex quadratic programs which builds upon and weaves together the proximal point algorithm and a damped semismooth Newton method. The outer proximal regularization yields a numerically stable method, and we interpret the proximal operator as the unconstrained minimization of the primal-dual proximal augmented Lagrangian function. This allows the inner Newton scheme to exploit sparse symmetric linear solvers and multi-rank factorization updates. Moreover, the linear systems are always solvable independently from the problem data and exact linesearch can be performed. The proposed method can handle degenerate problems, provides a mechanism for infeasibility detection, and can exploit warm starting, while requiring only convexity. We present details of our open-source C implementation and report on numerical results against state-of-the-art solvers. QPDO proves to be a simple, robust, and efficient numerical method for convex quadratic programming.

Reference:

• De Marchi, A.: On a primal-dual Newton proximal method for convex quadratic programs. Comput Optim Appl 81, 369–395 (2022). DOI 10.1007/s10589-021-00342-y

An algorithm for equilibrium selection in generalized Nash equilibrium problems

Abstract:

Recently a new solution concept for generalized Nash equilibrium problems was pub-
lished by the author. This concept selects a reasonable equilibrium out of the typically
infinitely many. The idea is to model the process of finding a compromise by solving
parametrized generalized Nash equilibrium problems. In this paper we propose an
algorithmic realization of the concept. The model produces a solution path, which is
under suitable assumptions unique. The algorithm is a homotopy method that tries to
follow this path. We use s emismooth Newton steps as corrector steps in our algorithm
in order to approximately solve the generalized Nash equilibrium problems for each
given parameter. If we have a unique solution path, we need three additional theo-
retical assumptions: a stationarity result for the merit function, a coercivity condition
for the constraints, and an extended Mangasarian–Fromowitz constraint qualification.
Then we can prove convergence of our semismooth tracing algorithm to the unique
equilibrium to be selected. We also present convincing numerical results on a test
library of problems from literature. The algorithm also performs well on a number of
problems that do not satisfy all the theoretical assumptions.

Reference:

• Dreves, A.: An algorithm for equilibrium selection in generalized Nash equilibrium problems. Computational Optimization and Applications. (2019), DOI 10.1007/s10589-019-00086-w.

Structure Exploitation in an Interior-Point Method for Fully Discretized, State Constrained Optimal Control Problems

Abstract:

 We discuss a direct discretization method for state-constrained optimal control problems and an interior-point method, which is used to solve the resulting large-scale and sparse nonlinear optimization problems. The main focus of the paper is on the investigation of an efficient method to solve the occurring linear equations with saddle-point structure. To this end, we exploit the particular structure that arises from the optimal control problem and the discretization scheme and use a tailored linear algebra solver alglin in combination with a re-ordering of the saddle-point matrices. Numerical experiments for a simple optimal control problem show a significant speed-up compared to state-of-the-art sparse LU decomposition methods like MA57 or MUMPS in combination with Ipopt.

Reference:

• Huber, A.; Gerdts, M. & Bertolazzi, E. (2018). Structure Exploitation in an Interior-Point Method for Fully Discretized, State Constrained Optimal Control Problems Vietnam Journal of Mathematics, doi: https://doi.org/10.1007/s10013-018-0318-7 .

How to Select a Solution in Generalized Nash Equilibrium Problems

Abstract:

We propose a new solution concept for generalized Nash equilibrium prob-
lems. This concept leads, under suitable assumptions, to unique solutions, which are
generalized Nash equilibria and the result of a mathematical procedure modeling the
process of finding a compromise. We first compute the favorite strategy for each player,
if he could dictate the game, and use the best response on the others’ favorite strategies
as starting point. Then, we perform a tracing procedure, where we solve parametrized
generalized Nash equilibrium problems, in which the players reduce the weight on the
best possible and increase the weight on the current strategies of the others. Finally, we
definethelimitingpoints of this tracingprocedureas solutions. Under our assumptions,
the new concept selects one reasonable out of typically infinitely many generalized
Nash equilibria.

Reference:

• Dreves, A.: How to select a solution in generalized Nash equilibrium problems. J. Optim. Theory Appl. (online 2018), DOI 10.1007/s10957-018-1327-0.

An Optimal Control Problem for a Rotating Elastic Crane-Trolley-Load System

Sven-Joachim Kimmerle, Matthias Gerdts, Roland Herzog, IFAC Papers Online Volume 51, Issue 2,  (2018), 272-277 Link zur Verlagsseite

Abstract:

In this study we present an extension of a model of an elastic crane transporting a load by means of controlling the crane trolley motion and the crane rotation. In addition to the model considered in Kimmerle et al. (2017), we allow for rotations of the crane and include damping of the trolley and moments of inertia as well. We derive a fully coupled system of ordinary differential equations (ODE), representing the trolley and load (modelled as a pendulum), and partial differential equations (PDE), i.e. the linear elasticity equations for the deformed crane beam. The objective to be minimized is a linear combination of the terminal time, the control effort, the kinetic energy of the load, and penalty terms for the terminal conditions. We show the Fréchet-differentiability of the mechanical displacement field with respect to the location of the boundary condition that is moving. This is a crucial point for a further mathematical analysis on the existence of optimal controls and the derivation of necessary optimality conditions. Finally we present first results for the full time-optimal control of the extended model.

Reference:

• Kimmerle, S.-J., Gerdts M., Herzog R..: An Optimal Control Problem for a Rotating Elastic Crane-Trolley-Load System. IFAC Papers Online Volume 51, Issue 2, , 272-277, (2018), DOI: dx.doi.org/10.1016/j.ifacol.2018.03.047.

Optimal control of an elastic crane-trolley-load system - a case study for optimal control of coupled ODE-PDE systems

Sven-Joachim Kimmerle, Matthias Gerdts, R. Herzog, Mathematical and Computer Modelling of Dynamical Systems Link zur Verlagsseite

Abstract:

We present a mathematical model of a crane-trolley-load model, where the crane beam is subject to the partial differential equation (PDE) of static linear elasticity and the motion of the load is described by the dynamics of a pendulum that is fixed to a trolley moving along the crane beam. The resulting problem serves as a case study for optimal control of fully coupled partial and ordinary differential equations (ODEs). This particular type of coupled systems arises from many applications involving mechanical multi-body systems. We motivate the coupled ODE-PDE model, show its analytical well-posedness locally in time and examine the corresponding optimal control problem numerically by means of a projected gradient method with Broyden-Fletcher-Goldfarb-Shanno (BFGS) update.

Reference:

• Kimmerle S.-J., Gerdts M., Herzog R.: Optimal control of an elastic crane-trolley-load system - a case study for optimal control of coupled ODE-PDE systems. Mathematical and Computer Modelling of Dynamical Systems 24:2 (2018), 182-206, DOI: doi.org/10.1080/13873954.2017.1405046.

Dynamic Equilibrium of a Coupled ODE-PDE Problem for Surface Nanobubbles

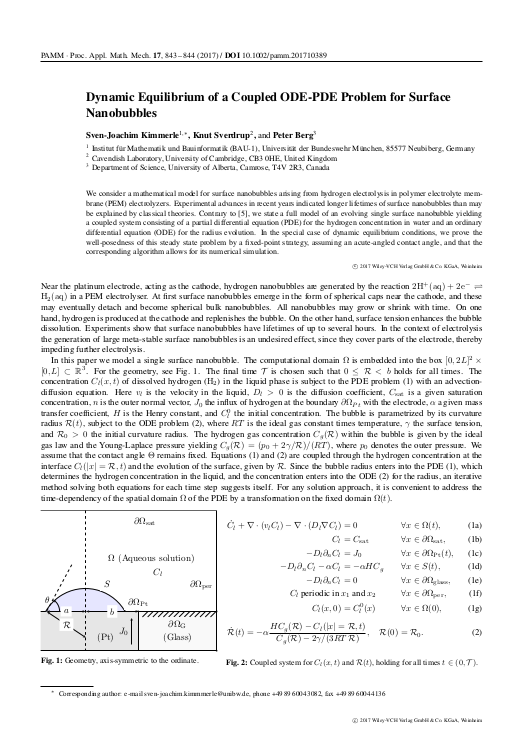Sven-Joachim Kimmerle, Knut Sverdrup, Peter Berg, Proc. Appl. Math. Mech.17, 843 – 844 (2017) Link zur Verlagsseite

Abstract:

 We consider a mathematical model for surface nanobubbles arising from hydrogen electrolysis in polymer electrolyte membrane (PEM) electrolyzers. Experimental advances in recent years indicated longer lifetimes of surface nanobubbles than may be explained by classical theories. Contrary to [5], we state a full model of an evolving single surface nanobubble yielding a coupled system consisting of a partial differential equation (PDE) for the hydrogen concentration in water and an ordinary differential equation (ODE) for the radius evolution. In the special case of dynamic equilibrium conditions, we prove the well-posedness of this steady state problem by a fixed-point strategy, assuming an acute-angled contact angle, and that the corresponding algorithm allows for its numerical simulation.

Reference:

• Kimmerle, S.-J., Sverdrup, K., Berg, P.: Dynamic Equilibrium of a Coupled ODE-PDE Problem for Surface Nanobubbles. Appl. Math. Mech.17, 843 – 844 (2017), 199-219, DOI: dx.doi.org/10.1002/pamm.201710389.

Line Search Globalization of a Semismooth Newton Method for Operator Equations in Hilbert Spaces with Applications in Optimal Control

Matthias Gerdts, Stefan Horn, Sven-Joachim Kimmerle, J. Ind. Manag. Optim. 13(1) (2017), 47-62 Link zur Verlagsseite

Abstract:

In recent years, the stability and lifetime of nanobubbles have raised new scientific questions as experimental techniques for nanobubble generation and measurements have advanced. In this contribution, we present a physical model for bulk nanobubbles and simulate their dissolution numerically using a rigorous treatment of the underlying governing equations. Additionally, we simulate surface nanobubbles with small contact angles replenished through hydrogen electrolysis at a platinum electrode, and discuss the relation between the mass transfer coefficient at the bubble surface and the supplied hydrogen flux at steady-state.

Reference:

• Gerdts, M., Horn, S., Kimmerle, S.-J.: Line Search Globalization of a Semismooth Newton Method for Operator Equations in Hilbert Spaces with Applications in Optimal Control, J. Ind. Manag. Optim. 13(1) (2017), 47-62, DOI: dx.doi.org/10.3934/jimo.2016003.

Computing all solutions of linear generalized Nash equilibrium problems

Abstract:

In this paper we consider linear generalized Nash equilibrium problems, i.e., the cost and the constraint functions of all players in a game are assumed to be linear. Exploiting duality theory, we design an algorithm that is able to compute the entire solution set of these problems and that terminates after finite time. We present numerical results on some academic examples as well as some economic market models to show effectiveness of our algorithm in small dimensions.

Reference:

• Dreves, A. (2017). Computing all solutions of linear generalized Nash equilibrium problems. Mathematical Methods of Operations Research, ISSN 1432-2994. Volume 85.  Number 2. doi:10.1007/s00186-016-0562-0. Springer.

Computational investigation of the stability and dissolution of nanobubbles

Knut Sverdrup, Sven-Joachim Kimmerle, Peter Berg, Appl. Math. Model. 49 (2017), 199-219 Link zur Verlagsseite

Abstract:

 In recent years, the stability and lifetime of nanobubbles have raised new scientific questions as experimental techniques for nanobubble generation and measurements have advanced. In this contribution, we present a physical model for bulk nanobubbles and simulate their dissolution numerically using a rigorous treatment of the underlying governing equations. Additionally, we simulate surface nanobubbles with small contact angles replenished through hydrogen electrolysis at a platinum electrode, and discuss the relation between the mass transfer coefficient at the bubble surface and the supplied hydrogen flux at steady-state.

Reference:

• Sverdrup, K., Kimmerle, S.-J., Berg, P.: Computational Investigation of the Stability and Dissolution of Nanobubbles. Appl. Math. Model. 49 (2017), 199-219, DOI: dx.doi.org/10.1016/j.apm.2017.05.006.

A generalized Nash equilibrium approach for optimal control problems of autonomous cars

Abstract:

We consider optimal control problems with ordinary differential equations that are coupled by shared, possibly nonconvex, constraints. For these problems, we use the generalized Nash equilibrium approach and provide a reformulation of normalized Nash equilibria as solutions to a single optimal control problem. By this reformulation, we are able to prove existence, and in some settings, exploiting convexity properties, we also get a limited number or even uniqueness of the normalized Nash equilibria. Then, we use our approach to discuss traffic scenarios with several autonomous vehicles, whose dynamics is described through differential equations, and the avoidance of collisions couples the optimal control problems of the vehicles. For the solution to the discretized problems, we prove strong convergence of the states and weak convergence of the controls. Finally, using existing optimal control software, we show that the generalized Nash equilibrium approach leads to reasonable results for a crossing scenario with different vehicle models.

Reference:

• Dreves, A., Gerdts M. (2017). A generalized Nash equilibrium approach for optimal control problems of autonomous cars. Optimal Control Applications and Methods. 1–17. ISSN: 1099-1514. doi:10.1002/oca.2348.

A dynamic programming MPC approach for automatic driving along tracks and its realization with online steering controllers

Abstract:

 The paper is concerned with the computation of trajectories along a given track for automatic cars using a dynamic programming approach in combination with a model predictive control strategy, which leads to a feedback control law providing a local reference trajectory. In addition, the setup of a testing environment using scale RC cars is described, which allows to verify and test control strategies in realtime. Results of experiments are presented that show the ability of the online controllers to track the reference paths at a good precision.

Reference:

• Huber, A. and Gerdts, M. (2017). A dynamic programming {MPC} approach for automatic driving along tracks and its realization with online steering controllers *. IFAC-PapersOnLine, 50(1), 8686 – 8691. doi:https://doi.org/10.1016/j.ifacol.2017.08.1529. URL http://www.sciencedirect.com/science/article/pii/S2405896317321158.

Modelling, simulation and optimization of an elastic structure under moving loads

Abstract:

We consider an elastic structure that is subject to moving loads representing e.g. heavy trucks on a bridge or a trolley on a crane beam. A model for the quasi-static mechanical behaviour of the structure is derived, yielding a coupled problem involving partial differential equations (PDE) and ordinary differential equations (ODE). The problem is simulated numerically and validated by comparison with a standard formula used in engineering. We derive an optimal policy for passing over potentially fragile bridges. In general, our problem class leads to optimal control problems subject to coupled ODE and PDE.

Reference:

• Kimmerle, S.-J.: Modelling, Simulation and Optimization of an Elastic Structure under Moving Loads, Proc. Appl. Math. Mech. 16(1) (2016), 697-698, DOI: 10.1002/pamm.201610337.

Necessary optimality conditions and a semi-smooth Newton approach for an optimal control problem of a coupled system of Saint-Venant equations and ordinary differential equations

Abstract:

In this article necessary optimality conditions for Saint-Venant equations coupled to ordinary differential equations (ODE) are derived rigorously. The Saint-Venant equations are first-order hyperbolic partial differential equations (PDE) and model here the fluid in a container that is moved by a truck that is subject to Newton's law of motion. The acceleration of the truck may be controlled. We describe the mathematical model and the corresponding tracking-type optimal control problem. First we prove existence and uniqueness for the coupled ODE-PDE problem locally in time. For sufficiently small times, we derive the first-order necessary optimality conditions in the corresponding function spaces. Furthermore we prove existence of optimal controls. The optimality system is formulated in the setting of a semi-smooth operator equation in Hilbert spaces which we solve numerically by a semi-smooth Newton method. We close with a numerical example for a typical driving maneuver.

Reference:

• Kimmerle, S.-J., Gerdts, M.: Necessary optimality conditions and a semi-smooth Newton approach for an optimal control problem of a coupled system of Saint-Venant equations and ordinary differential equations, Pure Appl. Funct. Anal. 1(2) (2016), 231-256 (Link http://www.ybook.co.jp/online2/oppafa/vol1/p231.html)

Optimal Control of ODEs and DAEs

Abstract:

Mathematische Optimierungsverfahren des Operations Research

Abstract:

Das Operations Research beschäftigt sich mit der Modellierung, qualitativen und quantitativen Analyse und algorithmischen Lösung von Entscheidungsproblemen. Es stellt Instrumente zur Analyse und Optimierung vernetzter Systeme bereit - u.a. in Wirtschaftsunternehmen, in der Städte- und Verkehrsplanung, Volkswirtschaft und Technik.

Es ist gleichermaßen Anwendungsfeld und Motivationsquelle für die in dieser Publikation behandelten Optimierungsverfahren. Deren Konzepte, theoretische Grundlagen und Eigenschaften werden ausführlich dargestellt. Zahlreiche Illustrationen unterstützen die Anschauung, viele vollständig durchgerechnete Beispiele tragen zum Verständnis bei und helfen beim Lösen der Übungsaufgaben.

Das Buch richtet sich an Studierende mathematischer Studiengänge, aber auch an mathematisch interessierte Studierende ingenieur- und wirtschaftswissenschaftlicher Studiengänge sowie an Wissenschaftler aus den Bereichen Mathematik, Wirtschaftsmathematik, Technomathematik, Wirtschafts- und Ingenieurwissenschaften, die an einer Einführung in Theorie und Verfahren der Optimierung interessiert sind.

• Klare und ausführliche Darstellung der mathematischen Optimierung
• Zahlreiche Beispiele, Übungsaufgaben und Testprogramme (auch online verfügbar)
• Gleichermaßen für Studierende und Praktiker geeignet