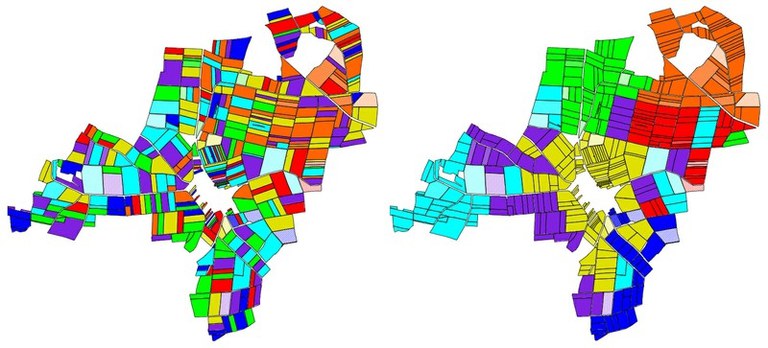
In many rural areas, a small number of farmers maintain a large number of small plots scattered over a wide area. This results in high travel costs and unprofitable use of the heavy machinery required. This could be remedied by land consolidation, which often leads to undesirable side effects. We develop mathematical models and algorithms for land consolidation that do not use the results of a classical land consolidation process.

The central idea of our methods is to preserve the structure of the plots in the region. Some of these plots are fixed by the farmers and the rest are reassigned combinatorially according to specific objective functions. During this process, each farmer will receive a series of parcels approximately equal to the original total size and value of the parcels. Since the plots differ in size and creditworthiness, we get a difficult clustering problem under constraints: The decision as to whether there is a different distribution of the plots so that these constraints are met represents an NP-complete problem.

Using combinatorial optimization methods, we obtain demonstrably good and efficient approximation algorithms. Within the framework of this project two goals are pursued: On the one hand the continuous improvement of the mathematical models, which represent the real problems of land consolidation, on the other hand the development of improved algorithms for these models.