Bei Interesse Prof. Mathias Richter (Inverse Probleme, Numerik), Dr. Robert Schmied (Künstliche Intelligenz, Kryptologie), Dr. José-Luis Marqués-Lopez (Dynamische Systeme, Quantencomputing) oder Dr. rer. nat. Johannes Pfefferer per E-Mail kontaktieren.
Themen für Bachelor- und Masterarbeiten
Themen
Numerische Simulation von Dynamischen Systemen
-
Chaotisches Verhalten im Lorenz System
Umgangssprachlich werden Chaos und Zufall oft gleichgesetzt, obwohl es sich um unterschiedliche Phänomene handelt. Ein tatsächlich zufälliges Geschehen hat objektiv keine Ursache – ob es so etwas wirklich gibt, ist umstritten. Oft modelliert man ein Geschehen bereits dann als zufällig, wenn man seine Einflussfaktoren bei allem Messaufwand nicht exakt erfassen und das Ergebnis deswegen nicht vorhersagen kann. Als chaotisch hingegen bezeichnet man ein System, das sich gemäß einer perfekt bekannten Dynamik verhält, dabei aber so empfindlich auf geänderte Anfangsbedingungen reagiert, dass deren Änderung ein völlig verändertes Verhalten nach sich zieht.
Die meist untersuchte Dynamik mit chaotischem Verhalten ist das Lorenz-System, beschrieben durch 3 Freiheitsgrade x1, x2 & x3 und kontrolliert durch 3 konstante (positive) Parameter σ, r & b
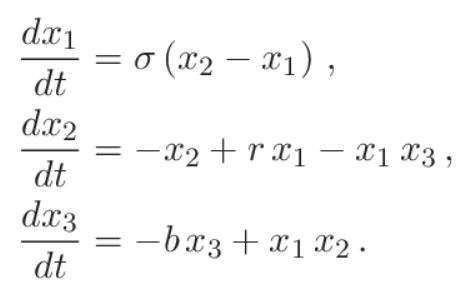
In der ursprünglichen Formulierung 1963 von Edward N. Lorenz stellt das System eine vereinfachte Modellierung der Luftgeschwindigkeit und Temperatur in einer Konvektionsströmung in der Atmosphäre dar, wobei x1 die kreisförmige Konvektionsgeschwindigkeit beschreibt und x2 & x3 die horizontale und vertikale Temperaturänderung. Die konstanten Parameter σ, r & b beinhalten jeweils die Information der Fluidviskosität, der Konvektionsstärke aufgrund von Temperaturgradienten und der horizontalen Längenskala (=Wellenlänge) der Konvektionsströmung. Berühmt ist das Lorenz-System für den sogenannten seltsamen Attraktor in Schmetterling-Form, welcher beim chaotischen Verhalten vorkommt. Aber dies ist nicht die einzige Erscheinung des Lorenz-Systems!
Die Aufgabe der Bachelorarbeit ist mittels MATLAB oder Octave (freie Version von MATLAB) einen Code zur numerischen Integration des Lorenz-Systems zu programmieren und die verschiedenen Verhalten je nach Werte σ, r & b zu untersuchen: Asymptotisch stabile Trajektorie, periodische Zyklen, quasiperiodisches Verhalten, Chaos. Die Aufgabe ist jedoch damit nicht abgeschlossen. Als ein anschaulicher Beweis, dass eine chaotische Bewegung ganz anders als eine zufällige Bewegung ist, wird mittels des entwickelten Codes eine Synchronisierung von 2 chaotische Lorenz-Systemen (Idee von Prof. Steven Strogatz, Cornell University) untersucht, ganz besonders unter welchen Bedingungen solch eine Synchronisierung erreicht wird.
-
Synchronisierung von verrauschten Oszillatoren (Kuramoto-Modell)
Die Synchronisierung von verschiedenen Aktuatoren, die in Wechselwirkung zueinander stehen (einfaches Beispiel: Applaudieren nach einem Konzert), ist eine häufige Erscheinung in der Natur: Ein besonders schönes Beispiel dabei ist die Synchronisierung von Glühwürmchen in der Paarungszeit. Synchronisierung kommt aber auch in technischen und menschlichen Netzwerken vor. Ein mathematisches Modell, das viele der Synchronisierungsmerkmale gut abbilden kann, ist das in 1975 durch Yoshiki Kuramoto eingeführtes nichtlineares Modell für N Oszillatoren, wo jeder Oszillator durch eine Winkelvariable θi beschrieben wird
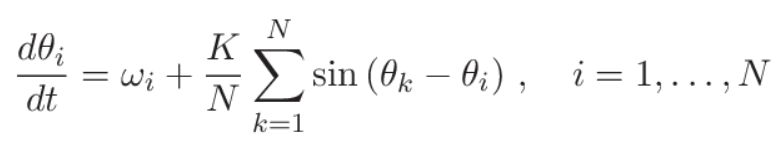
Dabei stellt ωi die Oszillator-Frequenz dar, welche vom Oszillator zum Oszillator leicht voneinander abweichen, und K ist die gemeinsame Kopplungsstärke der Oszillatoren unter sich. Dieses Modell zeigt weitere interessante Erscheinungen, wenn auch der Einfluss vom Rauschen eingebaut wird: Einerseits als additives Rauschen bei jedem Oszillator, und andererseits als leichte Streuung in der Kopplungsstärke K
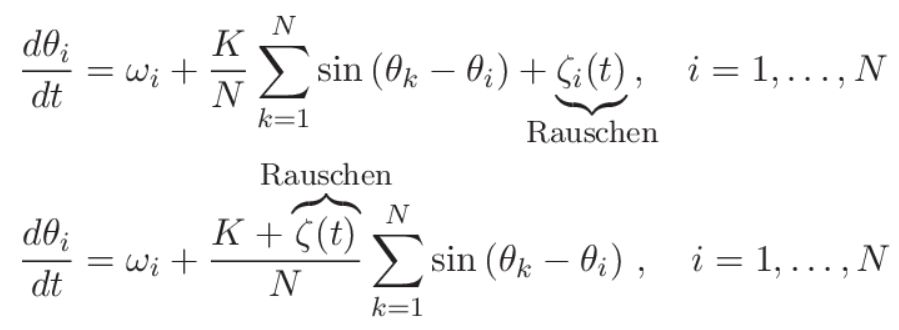
Die Aufgabe der Bachelorarbeit ist mittels MATLAB oder Octave (freie Version von MATLAB) einen Code zur numerischen Integration der 2 verrauschten Kuramoto-Modelle zu programmieren und anschließend das Synchronisierungsverhalten (oder die fehlende Synchronisierung) je nach Stärke des Rauschens (als weißes Rauschen angenommen) zu untersuchen. Dies wird begleitet durch eine einfache theoretische Analyse, welche das in den numerischen Lösungen beobachteten Verhalten validieren.
-
Stochastische Resonanz in einem Duffing-Oszillator
Beim Rauschen denkt man als „etwas Störendes“, welches das richtige Verhalten eines Systems nur abschwächen kann. Das muss nicht immer so sein (und ist es auch nicht), gerade bei nichtlinearen Systemen. Bei der Untersuchung des Klimawandels ist der Effekt vom schwachen Rauschen in Klima-Modellen sehr wichtig. Als Paradebeispiel ist das in 1983 durch Benzi, Parisi (Nobel-Preisträger in Physik im Jahr 2021), Sutera und Vulpiani eingeführte Modell der Stochastischen Resonanz. Damit wurden die sich wiederholenden Klima-Schwankungen auf der Erde mit einer Periode von ungefähr 100,000 Jahren mittels eines einfachen Modells eindrucksvoll erklärt. Dabei wurde entdeckt, dass selbst schwaches Rauschen eine verstärkende Wirkung in der Entstehung von Oszillationen (nur die ersten 20 Minuten des Videos) aufweisen kann.
Als Thema der Bachelorarbeit wird der sogenannte Duffing-Oszillator mit einer äußeren periodischen Anregung plus Rauschen untersucht

und mittels MATLAB oder Octave (freie Version von MATLAB) ein Code zur numerischen Integration dieser nichtlinearen Dynamik programmiert. Anschließend wird das Erscheinen der Stochastischen Resonanz je nach Stärke des Rauschens untersucht, wobei sowohl weißes Rauschen (d.h. zeitunkorreliertes Rauschen, „ohne Erinnerung“) wie farbiges Rauschen (d.h. zeitkorreliertes Rausches, „mit Erinnerung“) betrachtet werden.
Quantencomputing an einem echten Quantencomputer
-
Qubit-Kalibrierung und Shor-Algortihmus
RSA-Kryptosysteme stellen heute den Standard zur Daten-Verschlüsselung und digitalen Signieren in der Kommunikation dar. Diese basieren auf die Annahme, dass die Faktorisierung einer sehr großen Zahl eine so lange Zeit mit einem klassischen Computer benötigt, dass eine praktische Entschlüsselung nicht realisierbar ist. Die Veröffentlichung in 1994 durch Peter Shor von seinem nun weltberühmten Faktorisierungs-Algorithmus, womit ein (damals noch nicht vorhandener) Quantencomputer die verwendeten RSA-Kryptosysteme viel schneller „knacken“ kann, hat in den letzten 20 Jahren die Realisierung eines echten Quantencomputers enorm beschleunigt. Die aktuellen Quantencomputer stecken noch in den Kinderschuhen, da sie noch eine zu geringe Anzahl an Quantenbits (=Qubits) besitzen und diese Qubits ihre quantenmechanische Kohärenzeigenschaften schnell verlieren. Jedoch investieren große Konzerne wie IBM, Google oder Microsoft riesige Geldmengen in die weitere Entwicklung von solchen Maschinen: Ende dieses Jahres wird ein IBM-Quantencomputer erwartet, welcher die Grenze der 1000 supraleitenden Qubits überschreitet.
Das Thema der Bachelorarbeit ist zunächst zu verstehen, wie ein einzelner Qubit seine quantenmechanischen Eigenschaften mit der Zeit verliert. Dies wird anhand der Kalibrierung eines einzelnen Qubits in einem echten supraleitenden IBM-Quantencomputer untersucht. Als nächster Schritt werden die Details des Shor-Algorithmus ausgearbeitet und dieser Algorithmus bei einer geringen Anzahl an Qubits in einem echten IBM-Quantencomputer mittels Qiskit implementiert.
Kryptologie
-
Pohlig-Hellman-Verfahren zur Bestimmung des diskreten Logarithmus
Der diskrete Logarithmus ist die Umkehrfunktion der diskreten Exponentiation und zählt zu den schwierigen Problemen in der Zahlentheorie. Zu gegebenen natürlichen Zahlen a und x und einer Primzahl p lässt sich ax mod p einfach bestimmen. Sind jedoch natürliche Zahlen a, b und eine Primzahl p gegeben, so ist die Gleichung ax mod p= b nur schwer nach x auflösbar. Eine Möglichkeit ist das Pohlig-Hellman-Verfahren.
Die Aufgabe besteht darin, den mathematischen Hintergrund aufzuschreiben, diesen am Rechner umzusetzen und die Berechnungskomplexität nachzuvollziehen.
-
Pohlig-Hellman-Verfahren zur Verschlüsselung von Nachrichten
Auf Basis der Berechnungskomplexität des diskreten Logarithmus gibt es das Pohlig-Hellman-Verschlüsselungsverfahren. Zu gegebenen natürlichen Zahlen a und x und einer Primzahl p lässt sich ax mod p einfach bestimmen. Sind jedoch natürliche Zahlen a, b und eine Primzahl p gegeben, so ist die Gleichung ax mod p= b nur schwer nach x auflösbar. Dies nutzt man aus, um Nachrichten, die durch eine Zahl 0 ≤ M ≤ p kodiert sind, zu verschlüsseln.
Aufgabe ist es, den mathematischen Hintergrund des Verfahrens zur Ver- und Entschlüsselung zu beschreiben und am Rechner umzusetzen. Zudem sollen praktische Schwierigkeiten und Schwächen des Verfahrens aufgezeigt werden.
Künstliche Intelligenz
-
Erkennung von Buchstaben mit Faltungsnetzwerken
Faltungsnetzwerke eignen sich sehr gut zur Klassifikation von Bildern. Im Rahmen einer Bachelorarbeit erzeugen Sie einen Trainingsdatensatz in Form von Bildern zur Erkennung von Kleinbuchstaben des Alphabets und kümmern sich um die Konzeption und Umsetzung eines CNN zur Klassifikation der Bilder. -
Klassifikation von Audiodateien mit Hilfe von Faltungsnetzwerken
Zeitabhängige Audiodaten lassen sich mit Hilfe einer Zeit-Frequenz-Transformation in Frequenzdaten überführen. Aufgabe in dieser Bachelorarbeit ist es, Audiodateien so in Bilder zu transformieren, dass damit eine Klassifikation nach Musikgruppe oder Genre möglich wird. -
Handschrifterkennung mit rekurrenten neuronalen Netzen
Bei einer Handschrifterkennung geht es um die automatische Identifizierung und Umwandlung von handgeschriebenen Zeichen oder Texten in maschinenlesbaren Text. Aufgabe in dieser Bachelorarbeit ist es znächst, einen Trainingsdatensatz mit handgeschriebenem Text zu erzeugen. Dabei soll die zeitliche Abfolge der Schreibbewegung erfasst werden. Anschließend soll ein rekurrentes neuronales Netz (RNN) zur Erkennung der Handschrift konzipiert und umgesetzt werden. -
LSTM zur Vorhersage von Börsenkursen
Börsenkurse sind typische Beispiele von Zeitreihendaten, die häufig unerwarteten Schwankungen unterliegen. Aufgabe der Bachelorarbeit ist es, mit Hilfe eines LSTM die Börsenkurse einzelner Unternehmen vorherzusagen. Dabei sollen historische Kursdaten verwendet werden, um zukünftige Preisbewegungen vorherzusagen. -
Word2Vec-Modell zum Word-Embedding
Word2Vec ist ein bekanntes Modell zur Repräsentation von Tokens in einem hochdimensionalen reellen Vektorraum. Aufgabe der Bachelorarbeit ist es, ein solches Modell für deutschsprachige Tokens zu entwickeln. -
RNN vs. LSTM am Beispiel einer Reber-Grammatik
Eine Reber-Grammatik ist ein spezieller endlicher Automat, mit dem gültige Zeichenketten erzeugt werden können. Aufgabe der Bachelorarbeit ist es, auf Basis eines selbst erzeugten Trainingsdatensatzes mit sehr langen Zeichenketten ein RNN bzw. LSTM zu trainieren, welches das nächste Zeichen vorhersagt. Ein abschließender Vergleich der Güte der beiden Ansätze bietet sich an. -
Sportdatenanalyse mit Floodlight
Floodlight ist ein Tool zur Analyse von Spiel- und Leistungsdaten aus verschiedenen Sportarten, das im Rahmen eines Förderprojekts an der Sporthochschule Köln entwickelt wird. Aufgabe der Bachelorarbeit ist es, das Tool hinsichtlich der Eignung für KI-Methoden zu untersuchen. Insbesondere sollen räumliche und zeitliche Analysemöglichkeiten untersucht werden. -
Learning Nuggets für maschinelles Lernen
Learning Nuggets sind kurze Lerneinheiten zur Unterstützung der Lehre. Aufgabe der Bachelorarbeit ist es, ein Learning Nugget Ihrer Wahl in Form eines Lehrvideos im Umfeld der künstlichen Intelligenz zu erzeugen. -
DBSCAN-Algorithmus zur Clusteranalyse
Die Clusteranalyse zählt zu den Verfahren des nicht-überwachten Lernens. Eine Möglichkeit, Daten in Gruppen aufzuteilen besteht darin, Bereiche zu identifizieren, in denen Punkte konzentriert auftreten und diese von Bereichen mit anderen konzentrierten Daten zu trennen. Dabei werden Punkte gruppiert, die in der Nachbarschaft zueinander liegen. Als kleine Einleitung siehe das Vorlesungs-Video aus der Universität Bochum.
Aufgabe ist es, das Verfahren mathematisch zu notieren und am Rechner anhand von Beispielen umzusetzen. Dabei sollen Stärken und Schwächen des Verfahrens praktisch untersucht werden.
-
Lineare Diskriminanzanalyse
Die lineare Diskriminanzanalyse ist eines der ältesten immer noch gebräuchlichen Verfahren zur Klassifikation, behandelt somit Fragen des überwachten Lernens. Objekte, die als k-dimensionale metrische Merkmale gegeben sind, sind einer Klasse zugeordnet worden. Auf Grundlage dieser Zuordnung soll eine Funktion festgelegt werden, die nicht-zugeordnete Objekte einer Klasse zuweisen kann. Bei der linearen Diskriminanzanalyse werden die Daten auf Basis normalverteilter Klassen linear getrennt. Als kleine Einleitung siehe das folgende Vortrags-Video.
Aufgabe ist es, den mathematischen Hintergrund des Verfahrens zu beschreiben und anhand eines Beispiels am Rechner umzusetzen. Dabei soll auch auf Schwierigkeiten bei nicht linear trennbaren Daten eingegangen werden.