Chaotisches Verhalten im Lorenz System

Umgangssprachlich werden Chaos und Zufall oft gleichgesetzt, obwohl es sich um unterschiedliche Phänomene handelt. Ein tatsächlich zufälliges Geschehen hat objektiv keine Ursache – ob es so etwas wirklich gibt, ist umstritten. Oft modelliert man ein Geschehen bereits dann als zufällig, wenn man seine Einflussfaktoren bei allem Messaufwand nicht exakt erfassen und das Ergebnis deswegen nicht vorhersagen kann. Als chaotisch hingegen bezeichnet man ein System, das sich gemäß einer perfekt bekannten Dynamik verhält, dabei aber so empfindlich auf geänderte Anfangsbedingungen reagiert, dass deren Änderung ein völlig verändertes Verhalten nach sich zieht.

Die meist untersuchte Dynamik mit chaotischem Verhalten ist das Lorenz-System, beschrieben durch 3 Freiheitsgrade x₁, x₂ & x₃ und kontrolliert durch 3 konstante (positive) Parameter σ, r & b

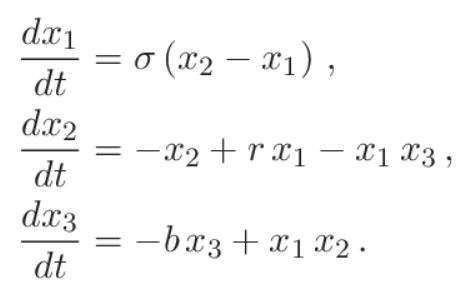
In der ursprünglichen Formulierung 1963 von Edward N. Lorenz stellt das System eine vereinfachte Modellierung der Luftgeschwindigkeit und Temperatur in einer Konvektionsströmung in der Atmosphäre dar, wobei x₁ die kreisförmige Konvektionsgeschwindigkeit beschreibt und x₂ & x₃ die horizontale und vertikale Temperaturänderung. Die konstanten Parameter σ, r & b beinhalten jeweils die Information der Fluidviskosität, der Konvektionsstärke aufgrund von Temperaturgradienten und der horizontalen Längenskala (=Wellenlänge) der Konvektionsströmung. Berühmt ist das Lorenz-System für den sogenannten seltsamen Attraktor in Schmetterling-Form, welcher beim chaotischen Verhalten vorkommt. Aber dies ist nicht die einzige Erscheinung des Lorenz-Systems!

Die Aufgabe der Bachelorarbeit ist mittels MATLAB oder Octave (freie Version von MATLAB) einen Code zur numerischen Integration des Lorenz-Systems zu programmieren und die verschiedenen Verhalten je nach Werte σ, r & b zu untersuchen: Asymptotisch stabile Trajektorie, periodische Zyklen, quasiperiodisches Verhalten, Chaos. Die Aufgabe ist jedoch damit nicht abgeschlossen. Als ein anschaulicher Beweis, dass eine chaotische Bewegung ganz anders als eine zufällige Bewegung ist, wird mittels des entwickelten Codes eine Synchronisierung von 2 chaotische Lorenz-Systemen (Idee von Prof. Steven Strogatz, Cornell University) untersucht, ganz besonders unter welchen Bedingungen solch eine Synchronisierung erreicht wird.

Synchronisierung von verrauschten Oszillatoren (Kuramoto-Modell)

Die Synchronisierung von verschiedenen Aktuatoren, die in Wechselwirkung zueinander stehen (einfaches Beispiel: Applaudieren nach einem Konzert), ist eine häufige Erscheinung in der Natur: Ein besonders schönes Beispiel dabei ist die Synchronisierung von Glühwürmchen in der Paarungszeit. Synchronisierung kommt aber auch in technischen und menschlichen Netzwerken vor. Ein mathematisches Modell, das viele der Synchronisierungsmerkmale gut abbilden kann, ist das in 1975 durch Yoshiki Kuramoto eingeführtes nichtlineares Modell für N Oszillatoren, wo jeder Oszillator durch eine Winkelvariable θ_i beschrieben wird

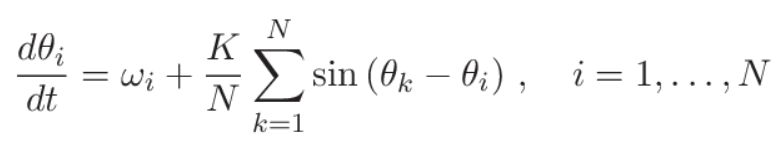
Dabei stellt ω_i die Oszillator-Frequenz dar, welche vom Oszillator zum Oszillator leicht voneinander abweichen, und K ist die gemeinsame Kopplungsstärke der Oszillatoren unter sich. Dieses Modell zeigt weitere interessante Erscheinungen, wenn auch der Einfluss vom Rauschen eingebaut wird: Einerseits als additives Rauschen bei jedem Oszillator, und andererseits als leichte Streuung in der Kopplungsstärke K

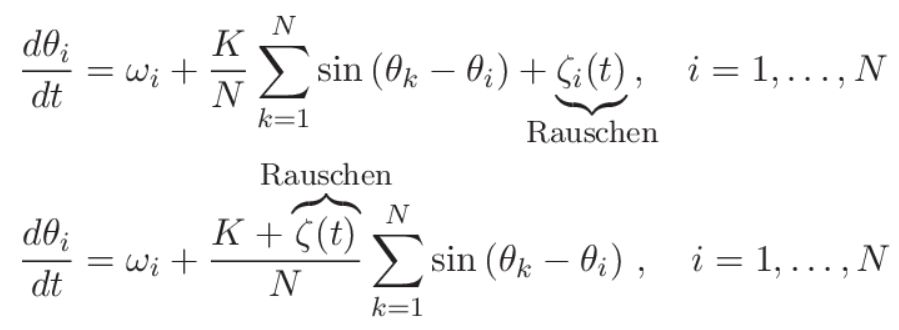
Die Aufgabe der Bachelorarbeit ist mittels MATLAB oder Octave (freie Version von MATLAB) einen Code zur numerischen Integration der 2 verrauschten Kuramoto-Modelle zu programmieren und anschließend das Synchronisierungsverhalten (oder die fehlende Synchronisierung) je nach Stärke des Rauschens (als weißes Rauschen angenommen) zu untersuchen. Dies wird begleitet durch eine einfache theoretische Analyse, welche das in den numerischen Lösungen beobachteten Verhalten validieren.

Stochastische Resonanz in einem Duffing-Oszillator

Beim Rauschen denkt man als „etwas Störendes“, welches das richtige Verhalten eines Systems nur abschwächen kann. Das muss nicht immer so sein (und ist es auch nicht), gerade bei nichtlinearen Systemen. Bei der Untersuchung des Klimawandels ist der Effekt vom schwachen Rauschen in Klima-Modellen sehr wichtig. Als Paradebeispiel ist das in 1983 durch Benzi, Parisi (Nobel-Preisträger in Physik im Jahr 2021), Sutera und Vulpiani eingeführte Modell der Stochastischen Resonanz. Damit wurden die sich wiederholenden Klima-Schwankungen auf der Erde mit einer Periode von ungefähr 100,000 Jahren mittels eines einfachen Modells eindrucksvoll erklärt. Dabei wurde entdeckt, dass selbst schwaches Rauschen eine verstärkende Wirkung in der Entstehung von Oszillationen (nur die ersten 20 Minuten des Videos) aufweisen kann.

Als Thema der Bachelorarbeit wird der sogenannte Duffing-Oszillator mit einer äußeren periodischen Anregung plus Rauschen untersucht

und mittels MATLAB oder Octave (freie Version von MATLAB) ein Code zur numerischen Integration dieser nichtlinearen Dynamik programmiert. Anschließend wird das Erscheinen der Stochastischen Resonanz je nach Stärke des Rauschens untersucht, wobei sowohl weißes Rauschen (d.h. zeitunkorreliertes Rauschen, „ohne Erinnerung“) wie farbiges Rauschen (d.h. zeitkorreliertes Rausches, „mit Erinnerung“) betrachtet werden.